题目内容
如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值( )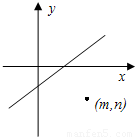
A.与C同号
B.与A同号
C.与B同号
D.与A,B均同号
【答案】分析:先根据直线Ax+By+C=0(AB≠0)的斜截式得结合直线所在的位置得: ,
, ,AC<0.由于原点O与点(m,n)分在直线的两侧,Am+Bn+C的符号与C的符号相反,而AC<0.进行判断即可.
,AC<0.由于原点O与点(m,n)分在直线的两侧,Am+Bn+C的符号与C的符号相反,而AC<0.进行判断即可.
解答:解:直线Ax+By+C=0(AB≠0)化成斜截式得:
y=- x-
x-
由直线所在的位置得: ,
, ,AC<0.
,AC<0.
由于原点O与点(m,n)分在直线的两侧,
∴(A×0+B×0+C)(Am+Bn+C)<0,
∴Am+Bn+C的符号与C的符号相反,而AC<0.
则Am+Bn+C的值与A同号
故选B.
点评:本题考查二无一次不等式的几何意义,解题时要注意特殊值法的合理运用及二元一次不等式(组)表示的平面区域.
 ,
, ,AC<0.由于原点O与点(m,n)分在直线的两侧,Am+Bn+C的符号与C的符号相反,而AC<0.进行判断即可.
,AC<0.由于原点O与点(m,n)分在直线的两侧,Am+Bn+C的符号与C的符号相反,而AC<0.进行判断即可.解答:解:直线Ax+By+C=0(AB≠0)化成斜截式得:
y=-
 x-
x-
由直线所在的位置得:
 ,
, ,AC<0.
,AC<0.由于原点O与点(m,n)分在直线的两侧,
∴(A×0+B×0+C)(Am+Bn+C)<0,
∴Am+Bn+C的符号与C的符号相反,而AC<0.
则Am+Bn+C的值与A同号
故选B.
点评:本题考查二无一次不等式的几何意义,解题时要注意特殊值法的合理运用及二元一次不等式(组)表示的平面区域.

练习册系列答案
相关题目
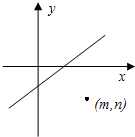 如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值( )
如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值( )| A、与C同号 | B、与A同号 | C、与B同号 | D、与A,B均同号 |
 如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值
如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值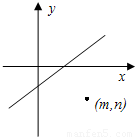
 A.与A同号,与B同号
A.与A同号,与B同号