题目内容

已知不等式ax²+2x-1＞0的解集是A，若（3，4）⊆A，则实数a的取值范围是________．

$\text{[math]}$
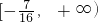
分析：本题中参数a的位置在最高次项上，故不等式相关函数的图象形状不确定，需要对参数a的范围进行讨论才能确定相应函数性质，结合函数的图象转化为参数a的不等式求出其范围，因是分类探究其范围，故最后的结果要并起来．
解答：当a=0时，不等式变为2x-1＞0，故A=（ $\text{[math]}$ ，+∞），满足（3，4）⊆A，故a=0可取；
当a＞0时，不等式ax²+2x-1＞0相应函数的对称轴是x=- $\text{[math]}$ ＜0，故欲使（3，4）⊆A，只需9a+5≥0，此式恒成立，故a＞0可取；
当a＜0时，不等式ax²+2x-1＞0相应函数的图象开口向下，故只需区间（3，4）两端点的函数值大于等于零，即间 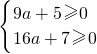$\text{[math]}$ 解得a≥- $\text{[math]}$ ．
综上知实数a的取值范围是[- $\text{[math]}$ ，+∞）
故应填[- $\text{[math]}$ ，+∞）
点评：本考点是一元二次不等式的应用，其特点是已知解集的结构，求参数的范围，本题中因为参数的位置比较特殊，故要分为三种情况进行讨论，这使得本题在解题运算上有一定的难度．