Question

解不等式.

Answer 1

解法一:原不等式的解是由下面两个不等式组的解集的并集构成.

(1)

(2)

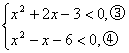
    由①解得{x|x＜-3或x＞1},

    由②解得{x|x＜-2或x＞3},

    ∴不等式组（1）的解集是{x|x＜-3或x＞3}.

    由③解得{x|-3＜x＜1},

    由④解得{x|-2＜x＜3},

    ∴不等式组（2）的解集是{x|-2＜x＜1}.

    综上，由不等式组（1）（2）的解集可得原不等式的解集是{x|x＜-3或-2＜x＜1或x＞3}.

解法二：原不等式可化为

令y=

    函数y的分子、分母各因式的根（从小到大排列）是-3，-2,1,3.

    现用四个根将x的取值范围分为五个区间：x＜-3,-3＜x＜-2,-2＜x＜1,1＜x＜3,x＞3.

    函数y在上述区间取值时，函数值的符号如下图（在x轴上方为正，在x轴下方为负）.

∵y＞0,由图可知，原不等式的解集是

{x|x＜-3或-2＜x＜1或x＞3}.