题目内容
B地在A地的正东方向4千米处,C地在B地的北偏东45°的 千米处.有一直线型的马路l过C地且与线段BC垂直,现欲在马路l上造一个车站P.造一公里马路的费用为5万元,则修筑两条马路PA、PB的最低费用为________万元.
千米处.有一直线型的马路l过C地且与线段BC垂直,现欲在马路l上造一个车站P.造一公里马路的费用为5万元,则修筑两条马路PA、PB的最低费用为________万元.
20
分析:由题意知,所求问题可转化为“已知直线l,和直线l外两点A、B,在l上求一点P,使P到A、B两点的距离之和最小”;现在作出点B关于直线l的对称点D,连接AD,交l与点P,点P即为所求.
解答: 解:如图所示,以A为坐标原点,AB为x轴,建立直角坐标系,
解:如图所示,以A为坐标原点,AB为x轴,建立直角坐标系,
且AB=4,∠CBE=45°,直线l⊥BC,垂足为C;BC=2 ,延长BC至D,使CD=BC=2
,延长BC至D,使CD=BC=2 ,连接AD,交直线l与点P,则点P即为所求的点;
,连接AD,交直线l与点P,则点P即为所求的点;
在坐标系xoy中,已知点A(0,0),B(4,0);可求点C(6,2),D(8,4);
∴PA+PB=PA+PD=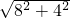 =4
=4 (千米);
(千米);
所以,修筑两条马路PA、PB的最低费用为:4 ×5=20
×5=20 (万元).
(万元).
故答案为:20 .
.
点评:本题借助于方向坐标,考查了平面几何中点关于直线对称的问题;解题时,借助于图形和直角坐标系,很容易解得结果.

分析:由题意知,所求问题可转化为“已知直线l,和直线l外两点A、B,在l上求一点P,使P到A、B两点的距离之和最小”;现在作出点B关于直线l的对称点D,连接AD,交l与点P,点P即为所求.
解答:
 解:如图所示,以A为坐标原点,AB为x轴,建立直角坐标系,
解:如图所示,以A为坐标原点,AB为x轴,建立直角坐标系,且AB=4,∠CBE=45°,直线l⊥BC,垂足为C;BC=2
 ,延长BC至D,使CD=BC=2
,延长BC至D,使CD=BC=2 ,连接AD,交直线l与点P,则点P即为所求的点;
,连接AD,交直线l与点P,则点P即为所求的点;在坐标系xoy中,已知点A(0,0),B(4,0);可求点C(6,2),D(8,4);
∴PA+PB=PA+PD=
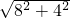 =4
=4 (千米);
(千米);所以,修筑两条马路PA、PB的最低费用为:4
 ×5=20
×5=20 (万元).
(万元).故答案为:20
 .
.点评:本题借助于方向坐标,考查了平面几何中点关于直线对称的问题;解题时,借助于图形和直角坐标系,很容易解得结果.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
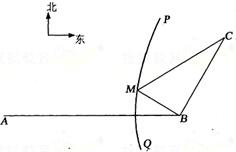 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是( )
A、(2
| ||
| B、5a万元 | ||
C、(2
| ||
D、(2
|
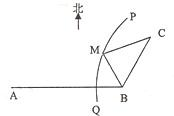 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元∕km、2a万元/km,那么修建这两条公路的总费用最低是
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元∕km、2a万元/km,那么修建这两条公路的总费用最低是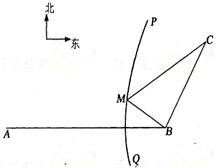 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km..现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.那么这两条公路MB、MC的路程之和最短是
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km..现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.那么这两条公路MB、MC的路程之和最短是