题目内容
已知函数
 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点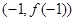 处的切线的斜率是
处的切线的斜率是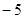 .
.
(1)求实数 的值;
的值;
(2)求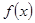 在区间
在区间 上的最大值;
上的最大值;
(3)对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在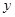 轴上?请说明理由.
轴上?请说明理由.
(1)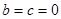 ;(2)
;(2) 在
在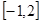 上的最大值为
上的最大值为 ;(3)对任意给定的正实数
;(3)对任意给定的正实数 ,曲线
,曲线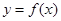 上总存在两点
上总存在两点 ,使得
,使得 是以
是以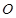 为直角顶点的直角三角形,且此三角形斜边的中点在y轴上.
为直角顶点的直角三角形,且此三角形斜边的中点在y轴上.
解析试题分析:(1)求实数 的值,由函数
的值,由函数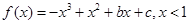 ,由图像过坐标原点
,由图像过坐标原点 ,得
,得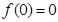 ,且根据函数在点
,且根据函数在点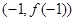 处的切线的斜率是
处的切线的斜率是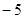 ,由导数几何意义可得
,由导数几何意义可得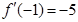 ,建立方程组,可确定实数
,建立方程组,可确定实数 的值,进而可确定函数的解析式;(2)求
的值,进而可确定函数的解析式;(2)求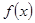 在区间
在区间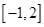 的最大值,因为
的最大值,因为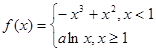 ,由于
,由于 是分段函数,可分段求最大值,最后确定最大值,当
是分段函数,可分段求最大值,最后确定最大值,当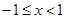 时,
时,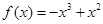 ,求导得,
,求导得, ,令
,令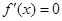 ,可得
,可得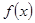 在
在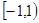 上的最大值为
上的最大值为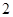 ,当
,当 时,
时, .对
.对 讨论,确定函数的单调性,即可求得结论;(3)这是探索性命题,可假设曲线
讨论,确定函数的单调性,即可求得结论;(3)这是探索性命题,可假设曲线 上存在两点
上存在两点 满足题设要求,则点
满足题设要求,则点 只能在
只能在 轴两侧.设
轴两侧.设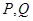 的坐标,由此入手能得到对任意给定的正实数
的坐标,由此入手能得到对任意给定的正实数 ,曲线
,曲线 上存在两点
上存在两点 使得
使得 是以
是以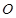 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在 轴上.
轴上.
试题解析:(1)当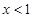 时,
时,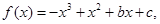 则
则 (1分)
(1分)
依题意,得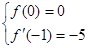 即
即 ,解得
,解得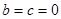 . (3分)
. (3分)
(2)由(1)知,
 ①当
①当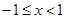 时
时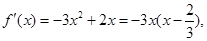 令
令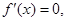 得
得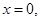 或
或 (4分)
(4分)
当 变化时
变化时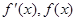 的变化情况如下表:
的变化情况如下表:
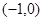
 0
0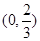

( 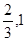 )
)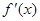
—  0
0
寒假衔接班寒假提优20天江苏人民出版社系列答案
宏翔文化3年中考2年模拟1年预测系列答案
初中毕业生升学模拟考试系列答案
过好寒假每一天系列答案
寒假作业中国地图出版社系列答案
中考复习攻略南京师范大学出版社系列答案
智多星归类复习测试卷系列答案
智多星模拟加真题测试卷系列答案
毕业升学考卷大集结系列答案
毕业升学冲刺必备方案系列答案
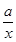 (x≠0,a∈R).
(x≠0,a∈R).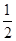 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R. ax3-
ax3-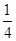 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.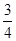 x2-bx+
x2-bx+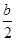 -
- -1.
-1.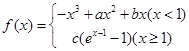 在
在 处存在极值.
处存在极值. 的值;
的值; 的图像上存在两点A,B使得
的图像上存在两点A,B使得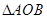 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在 轴上,求实数
轴上,求实数 的取值范围;
的取值范围; 时,讨论关于
时,讨论关于 的方程
的方程 的实根个数.
的实根个数.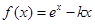 .
. ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围; ,
,