题目内容
某地区数学考试的成绩x服从正态分布,其密度函数曲线如下图.成绩x位于区间(52,68]的概率是多少?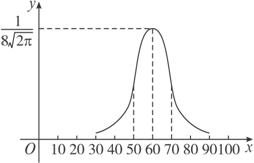
分析:这是道典型的由图形求函数,由函数求概率的题目,我们发现x—N(μ,σ2),其中μ=60,f(x)= ,
,
∴σ=8.而区间(52,68]关于x=μ对称,
∴P(52<x≤68)=P(60-8<x≤60+8)=P(μ-σ<x≤μ+σ)=0.682 6.
解:∵x服从正态分布,设其密度函数f(x)= 由图形知μ=60,顶点为(60,
由图形知μ=60,顶点为(60, ![]() ),∴σ=8.
),∴σ=8.
设x位于区间(52,68]上的概率为P(52<x≤68)=P(60-8<x≤60+8)=P(μ-σ<x≤μ+σ)=0.683.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
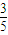 ,则此次考试成绩不低于90分的学生约有______人.
,则此次考试成绩不低于90分的学生约有______人.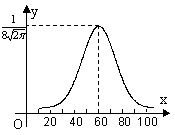 A.0.6826 B.0.9544 C.0.9974 D.0.3413
A.0.6826 B.0.9544 C.0.9974 D.0.3413