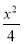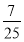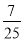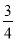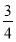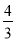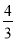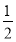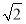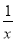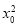Question

设f(x)＝a(x－5)2＋6ln x，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线与y轴相交于点(0,6)．

(1)确定a的值；

(2)求函数f(x)的单调区间与极值．

 

Answer 1

(1) a＝(2) f(x)在(0,2)，(3，＋∞)上为增函数；当2<x<3时，f′(x)<0，故f(x)在(2,3)上为减函数．f(x)在x＝2处取得极大值f(2)＝＋6ln 2，在x＝3处取得极小值f(3)＝2＋6ln 3.

【解析】(1)因f(x)＝a(x－5)2＋6ln x，

故f′(x)＝2a(x－5)＋令x＝1，得f(1)＝16a，f′(1)＝6－8a，

所以曲线y＝f(x)在点(1，f(1))处的切线方程为y－16a＝(6－8a)(x－1)，

由点(0,6)在切线上可得6－16a＝8a－6，故a＝.

(2)由(1)知，f(x)＝(x－5)2＋6ln x(x>0)，f′(x)＝x－5＋＝?

令f′(x)＝0，解得x1＝2，x2＝3.当0<x<2或x>3时，f′(x)>0，

故f(x)在(0,2)，(3，＋∞)上为增函数；

当2<x<3时，f′(x)<0，故f(x)在(2,3)上为减函数．

由此可知f(x)在x＝2处取得极大值f(2)＝＋6ln 2，在x＝3处取得极小值f(3)＝2＋6ln 3.