题目内容
已知△ABC中,2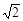 (sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为
(sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为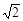 .(1)求∠C;(2)求△ABC面积的最大值.
.(1)求∠C;(2)求△ABC面积的最大值.
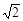 (sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为
(sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为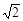 .(1)求∠C;(2)求△ABC面积的最大值.
.(1)求∠C;(2)求△ABC面积的最大值.(1)由2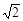 (sin2A-sin2C)=(a-b)·sinB得 2
(sin2A-sin2C)=(a-b)·sinB得 2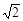 (
(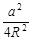 -
- )=
)=
(a-b)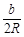 . 又∵R=
. 又∵R=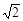 ,∴a2-c2=ab-b2.∴a2+b2-c2=ab.∴cosC=
,∴a2-c2=ab-b2.∴a2+b2-c2=ab.∴cosC= =
=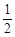 . 又∵0°<C<180°,∴C=60°.(6分)
. 又∵0°<C<180°,∴C=60°.(6分)
(2)S=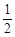 absinC=
absinC=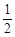 ×
× ab=2
ab=2 sinAsinB=2
sinAsinB=2 sinAsin(120°-A)=
sinAsin(120°-A)=
2 sinA(sin120°cosA-cos120°sinA)=3sinAcosA+
sinA(sin120°cosA-cos120°sinA)=3sinAcosA+ sin2A=
sin2A=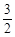 sin2A
sin2A
 cos2A+
cos2A+ =
= sin(2A-30°)+
sin(2A-30°)+ . ∴当2A=120°,即A=60°时,Smax=
. ∴当2A=120°,即A=60°时,Smax=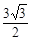
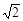 (sin2A-sin2C)=(a-b)·sinB得 2
(sin2A-sin2C)=(a-b)·sinB得 2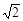 (
(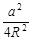 -
- )=
)=(a-b)
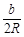 . 又∵R=
. 又∵R=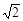 ,∴a2-c2=ab-b2.∴a2+b2-c2=ab.∴cosC=
,∴a2-c2=ab-b2.∴a2+b2-c2=ab.∴cosC= =
=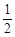 . 又∵0°<C<180°,∴C=60°.(6分)
. 又∵0°<C<180°,∴C=60°.(6分)(2)S=
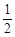 absinC=
absinC=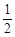 ×
× ab=2
ab=2 sinAsinB=2
sinAsinB=2 sinAsin(120°-A)=
sinAsin(120°-A)=2
 sinA(sin120°cosA-cos120°sinA)=3sinAcosA+
sinA(sin120°cosA-cos120°sinA)=3sinAcosA+ sin2A=
sin2A=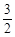 sin2A
sin2A  cos2A+
cos2A+ =
= sin(2A-30°)+
sin(2A-30°)+ . ∴当2A=120°,即A=60°时,Smax=
. ∴当2A=120°,即A=60°时,Smax=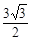
略

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
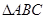 中,
中,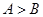 ,且
,且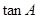 与
与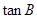 是方程
是方程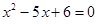 的两个根.
的两个根. 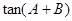 的值;
的值;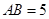 ,求
,求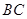 的长.
的长. 中,
中, ,
, ,
, ,那么
,那么 等于( )
等于( )



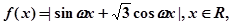 又
又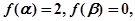 且
且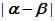 的最小值等于
的最小值等于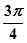 ,则正数
,则正数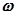 的值为( )
的值为( )



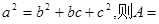 ( )
( ) =4,
=4,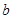 =6,
=6, =
= ,则角C为( )
,则角C为( )

 的内角
的内角 的对边分别为
的对边分别为 ,
, ,
, ,求
,求 .
.