Question

（本小题满分12分）

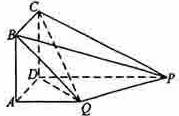如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．

（I）证明：平面PQC⊥平面DCQ；

（II）求二面角Q—BP—C的余弦值．

Answer 1

解：

如图，以D为坐标原点，线段DA的长为单位长，射线DA为x轴的正半轴建立空间直角坐标系D—xyz.

   （I）依题意有Q（1，1，0），C（0，0，1），P（0，2，0）.

则

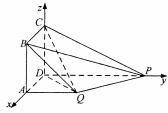所以

即PQ⊥DQ，PQ⊥DC.

故PQ⊥平面DCQ.

又PQ平面PQC，所以平面PQC⊥平面DCQ.  …………6分

   （II）依题意有B（1，0，1），

设是平面PBC的法向量，则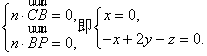

因此可取

设m是平面PBQ的法向量，则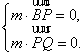

可取

故二面角Q—BP—C的余弦值为   ………………12分