题目内容
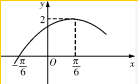 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<| π | 2 |
(1)求f(x)的解析式.
(2)求f(x)的对称轴方程,对称中心坐标.
(3)求f(x)的单调区间及取得最大值的x值.
分析:(1)由函数的图象得出A,求出函数的半周期,从而得出ω,代入最高点坐标求出φ,得函数的解析式;
(2)由(1)利用正弦函数的对称轴方程求解函数的对称轴方程,对称中心坐标求解对称中心坐标.
(3)通过正弦函数的单调区间求解函数的单调递区间,利用正弦函数的最值直接求解x的值.
(2)由(1)利用正弦函数的对称轴方程求解函数的对称轴方程,对称中心坐标求解对称中心坐标.
(3)通过正弦函数的单调区间求解函数的单调递区间,利用正弦函数的最值直接求解x的值.
解答:解:(1)由题设知,A=3,T=4×(
+
)=π,∴ω=2,
∴f(x)=3sin(2x+φ),∵3sin(2×
+φ)=3,∴sin(
+φ)=1,
∴
+φ=
,∴φ=
,∴f(x)=3sin(2x+
);
(2)由2x+
=kπ+
,得x=
+
,k∈Z,
∴函数f(x)的对称轴方程为x=
+
(k∈Z),
由2x+
=kπ得x=
-
(k∈Z),
∴函数f(x)的对称中心坐标为(
-
,0)(k∈Z);
(3)
+2kπ≤2x+
≤2kπ+
,k∈Z,
得
+kπ≤x≤kπ+
,k∈Z,
故函数的单调增区间是[
+kπ,kπ+
], k∈Z.
当2x+
=2kπ+
,k∈Z,解得x=kπ+
,k∈Z,
函数f(x)取得最大值.
| π |
| 6 |
| π |
| 6 |

∴f(x)=3sin(2x+φ),∵3sin(2×
| π |
| 6 |
| π |
| 3 |
∴
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
(2)由2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
∴函数f(x)的对称轴方程为x=
| kπ |
| 2 |
| π |
| 6 |
由2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
∴函数f(x)的对称中心坐标为(
| kπ |
| 2 |
| π |
| 12 |
(3)
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
得
| π |
| 6 |
| 2π |
| 3 |
故函数的单调增区间是[
| π |
| 6 |
| 2π |
| 3 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
函数f(x)取得最大值.
点评:求y=Asin(ωx+φ)的解析式,条件不管以何种方式给出,一般先求A,再求ω,最后求φ;求y=Asin(ωx+φ)的单调递增区间、对称轴方程、对称中心坐标时,要把ωx+φ看作整体,分别代入正弦函数的单调递增区间、对称轴方程、对称中心坐标分别求出x,这儿利用整体的思想;求y=Asin(ωx+φ)的最大值,需要借助正弦函数的最大值的求解方法即可.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
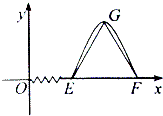 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,