题目内容
已知平面内点M(-3,2),N(5,-4),l是经过点A(-1,-2)且与MN垂直的直线,动点P(x,y)满足
•
=-21.
(1)求直线l的方程与动点P的轨迹Σ的方程;
(2)在轨迹Σ上任取一点P,求P在直线l右下方的概率.
| PM |
| PN |
(1)求直线l的方程与动点P的轨迹Σ的方程;
(2)在轨迹Σ上任取一点P,求P在直线l右下方的概率.
分析:(1)求出直线l的斜率,利用点斜式可得方程,利用向量的数量积运算,可求动点P的轨迹Σ的方程;
(2)因为P在直线l右下方,所以P在优弧EF上,故求P在直线l右下方的概率.
(2)因为P在直线l右下方,所以P在优弧EF上,故求P在直线l右下方的概率.
解答:解:(1)由题意kMN=
=-
,kl=-
=
…(2分),
所以直线l的方程为y-(-2)=
[x-(-1)],即4x-3y-2=0…(3分),
又
=(-3-x,2-y),
=(5-x,-4-y)…(4分),
由
•
=-21得(-3-x)(5-x)+(2-y)(-4-y)=-21…(5分),
整理得,轨迹方程为(x-1)2+(y+1)2=4…(6分)
(2)轨迹Σ是圆心为C(1,-1)、半径r=2的圆…(7分),
C到直线l的距离d=
=1…(8分),
所以d=1<r,直线l与圆Σ相交…(9分),
设交点为E、F,则cos
∠ECF=
=
…(10分),所以∠ECF=
…(11分),
所以圆C的优弧EF的长为r•(2π-∠ECF)=
…(12分),
因为P在直线l右下方,所以P在优弧EF上,所求概率为P=
=
…(14分)
| -4-2 |
| 5-(-3) |
| 3 |
| 4 |
| 1 |
| kMN |
| 4 |
| 3 |
所以直线l的方程为y-(-2)=
| 4 |
| 3 |
又
| PM |
| PN |
由
| PM |
| PN |
整理得,轨迹方程为(x-1)2+(y+1)2=4…(6分)
(2)轨迹Σ是圆心为C(1,-1)、半径r=2的圆…(7分),
C到直线l的距离d=
| 4×1-3×(-1)-2 |
| 5 |
所以d=1<r,直线l与圆Σ相交…(9分),
设交点为E、F,则cos
| 1 |
| 2 |
| d |
| r |
| 1 |
| 2 |
| 2π |
| 3 |
所以圆C的优弧EF的长为r•(2π-∠ECF)=
| 8π |
| 3 |
因为P在直线l右下方,所以P在优弧EF上,所求概率为P=
| ||
| 2πr |
| 2 |
| 3 |
点评:本题考查轨迹方程,考查概率知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
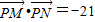 .
.