题目内容
(2006•西城区二模)在棱长为1的正方体ABCD-A1B1C1D1中,点D到平面ACD1的距离为
,若点P为△BCD的重心,则D1P与平面ADD1A1所成角的大小为
| ||
| 3 |
| ||
| 3 |
arctan
| ||
| 5 |
arctan
.
| ||
| 5 |
分析:由正方体的棱长求出ACD1的边长,利用等积法求点D到平面ACD1的距离;找出△BCD的重心P,作出D1P与平面ADD1A1所成角,利用三角形中心的性质求出对应的一些边长,最后通过解直角三角形求D1P与平面ADD1A1所成角的大小.
解答: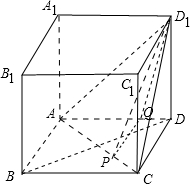 解:如图,
解:如图,
∵ABCD-A1B1C1D1为正方体,且棱长为1,
∴AC=CD1=AD1=
,
则S△ACD1=
×
×
=
.
设点D到平面ACD1的距离为h,
则
×
×1×1×1=
×
h,
解得h=
∵P为为△BCD的重心,∴PC=
AC,AP=
AC.
过P作PQ∥CD交AD于Q,则AQ⊥m面ADD1,D1Q,
则∠PD1Q为D1P与平面ADD1A1所成角.
PQ=
CD=
,QD=
,QD1=
=
.
∴tan∠PD1Q=
=
=
.
∴D1P与平面ADD1A1所成角的大小为arctan
.
故答案为
,arctan
.
 解:如图,
解:如图,∵ABCD-A1B1C1D1为正方体,且棱长为1,
∴AC=CD1=AD1=
| 2 |
则S△ACD1=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
设点D到平面ACD1的距离为h,
则
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
解得h=
| ||
| 3 |
∵P为为△BCD的重心,∴PC=
| 1 |
| 3 |
| 2 |
| 3 |
过P作PQ∥CD交AD于Q,则AQ⊥m面ADD1,D1Q,
则∠PD1Q为D1P与平面ADD1A1所成角.
PQ=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
12+(
|
| ||
| 3 |
∴tan∠PD1Q=
| PQ |
| D1Q |
| ||||
|
| ||
| 5 |
∴D1P与平面ADD1A1所成角的大小为arctan
| ||
| 5 |
故答案为
| ||
| 3 |
| ||
| 5 |
点评:本题考查了直线与平面所成的角,考查了空间中的点、线、面间的距离,考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
相关题目
