题目内容
求下列函数的值域:
(1) y=x-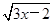 ;
;
(2) y=x2-2x-3,x∈(-1,4];
(3) y=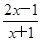 ,x∈[3,5];
,x∈[3,5];
(4) y=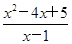 (x>1).
(x>1).
(1) y=x-
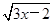 ;
;(2) y=x2-2x-3,x∈(-1,4];
(3) y=
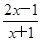 ,x∈[3,5];
,x∈[3,5];(4) y=
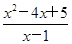 (x>1).
(x>1).(1)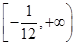 (2)[-4,5].(3)
(2)[-4,5].(3)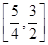 (4)[2
(4)[2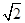 -2,+∞).
-2,+∞).
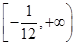 (2)[-4,5].(3)
(2)[-4,5].(3)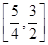 (4)[2
(4)[2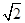 -2,+∞).
-2,+∞).(1) (换元法)设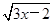 =t,t≥0,则y=
=t,t≥0,则y=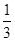 (t2+2)-t=
(t2+2)-t=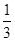
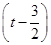 2-
2-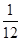 ,当t=
,当t=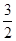 时,y有最小值-
时,y有最小值-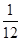 ,故所求函数的值域为
,故所求函数的值域为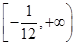 .
.
(2) (配方法)配方,得y=(x-1)2-4,因为x∈(-1,4],结合图象知,所求函数的值域为[-4,5].
(3) (解法1)由y=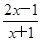 =2-
=2-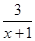 ,结合图象知,函数在[3,5]上是增函数,所以ymax=
,结合图象知,函数在[3,5]上是增函数,所以ymax=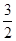 ,ymin=
,ymin=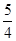 ,故所求函数的值域是
,故所求函数的值域是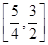 .
.
(解法2)由y=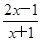 ,得x=
,得x=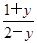 .因为x∈[3,5],所以3≤
.因为x∈[3,5],所以3≤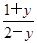 ≤5,解得
≤5,解得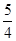 ≤y≤
≤y≤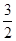 ,
,
即所求函数的值域是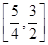 .
.
(4) (基本不等式法)令t=x-1,则x=t+1(t>0),
所以y=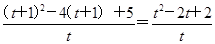 =t+
=t+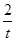 -2(t>0).
-2(t>0).
因为t+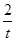 ≥2
≥2 =2
=2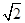 ,当且仅当t=
,当且仅当t=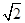 ,即x=
,即x=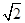 +1时,等号成立,
+1时,等号成立,
故所求函数的值域为[2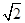 -2,+∞).
-2,+∞).
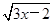 =t,t≥0,则y=
=t,t≥0,则y=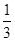 (t2+2)-t=
(t2+2)-t=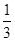
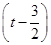 2-
2-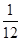 ,当t=
,当t=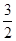 时,y有最小值-
时,y有最小值-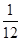 ,故所求函数的值域为
,故所求函数的值域为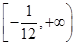 .
.(2) (配方法)配方,得y=(x-1)2-4,因为x∈(-1,4],结合图象知,所求函数的值域为[-4,5].
(3) (解法1)由y=
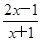 =2-
=2-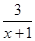 ,结合图象知,函数在[3,5]上是增函数,所以ymax=
,结合图象知,函数在[3,5]上是增函数,所以ymax=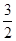 ,ymin=
,ymin=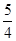 ,故所求函数的值域是
,故所求函数的值域是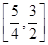 .
.(解法2)由y=
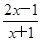 ,得x=
,得x=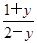 .因为x∈[3,5],所以3≤
.因为x∈[3,5],所以3≤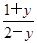 ≤5,解得
≤5,解得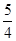 ≤y≤
≤y≤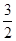 ,
,即所求函数的值域是
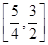 .
.(4) (基本不等式法)令t=x-1,则x=t+1(t>0),
所以y=
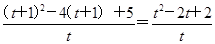 =t+
=t+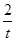 -2(t>0).
-2(t>0).因为t+
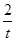 ≥2
≥2 =2
=2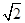 ,当且仅当t=
,当且仅当t=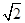 ,即x=
,即x=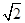 +1时,等号成立,
+1时,等号成立,故所求函数的值域为[2
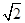 -2,+∞).
-2,+∞).
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 定义域是__ ;
定义域是__ ; 的定义域为( )
的定义域为( )



 的值域为________.
的值域为________. 的值域为____________.
的值域为____________. -
- 的定义域是( )
的定义域是( ) 的定义域是( )
的定义域是( )



 ,对于
,对于 ,若
,若 ,满足
,满足 ,则
,则 的取值范围是( )
的取值范围是( ) 


