题目内容
若数列|an|存在极限,那么这极限是惟一的。请给予证明。
答案:
解析:
提示:
解析:
用反证法证明:该数列{an}有两个不同的极限a,b据极限定义,对任意正数e,存在正整数N1,使当n>N1时, 同样,对上述正数e,存在正整数N2,使当n>N2时 ∴ |
提示:
反证法。 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
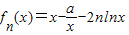 恒存在极小值an(a>0),
恒存在极小值an(a>0), 的极小值点.
的极小值点. 的极小值点.
的极小值点.