题目内容
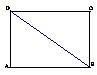 已知矩形ABCD中,AB=
已知矩形ABCD中,AB=| 2 |
(I)求证:DA⊥面ABC;
(II)求二面角C-BD-A平面角的大小.
分析:(I)由已知AC=AD=1,DC=AB=
可得AC⊥AD①AD⊥AB②,由①②根据线面垂直的判定定理可证DA⊥面ABC
(II)(法一:三垂线法)由(I)可得平面ABC⊥平面ABD.取AB中点M,则面面垂直的性质定理可得CM⊥平面ABD,作MN⊥BD,从而可用三垂线法作出二面角的平面角∠CMN,再直角三角形△CMN中求解
(法二:定义法)同法一可得CM⊥平面ABD,由已知AB⊥AC,考虑取BD的中点H,则可得MN∥AD,从而有MH⊥AB,然后利用空间向量的方法:分别以AB,MH,MC为x,y,z轴建立空间直角坐标系,设平面BCD的一个法向量
,平面ABD的一个法向量为
,代入公式cosθ=
求解即可.
| 2 |
(II)(法一:三垂线法)由(I)可得平面ABC⊥平面ABD.取AB中点M,则面面垂直的性质定理可得CM⊥平面ABD,作MN⊥BD,从而可用三垂线法作出二面角的平面角∠CMN,再直角三角形△CMN中求解
(法二:定义法)同法一可得CM⊥平面ABD,由已知AB⊥AC,考虑取BD的中点H,则可得MN∥AD,从而有MH⊥AB,然后利用空间向量的方法:分别以AB,MH,MC为x,y,z轴建立空间直角坐标系,设平面BCD的一个法向量
| n |
| m |
| ||||||
|
|
解答: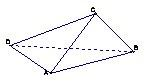 解:(I)∵DA=AC=1,DC=
解:(I)∵DA=AC=1,DC=
,
∴AC2+AD2=CD2,∴DA⊥AC.(3分)
又∵DA⊥AB,∴AB∩AC=A∴DA⊥平面ABC.(6分)
(II)方法一:取AB中点M,连CM,
过M作MN⊥BD交BD于N,
连CN.∵CA=CB=1,∴CM⊥AB,
∵DA?平面ABD,DA⊥平面ABC,
∴平面ABC⊥平面ABD.(8分)
∴CM⊥平面ABD,∴CM⊥BD.
又∵MN⊥BD,MN∩CM=M
∴BD⊥平面CMN,
∴∠CNM为二面角C-BD-A的平面角.(10分)
∴MN=
•1=
,CM=
,
tan∠CNM=
=
,∴∠CNM=60°,
故二面角C-BD-A平面角的度数为60°.(12分)
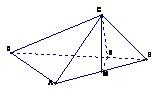 方法二:取AB中点M,连CM.
方法二:取AB中点M,连CM.
∵AC=AB=1,∴CM⊥AB.
又∵平面ABC⊥平面ABD,∴CM⊥平面ABD.
取BD中点H,∴MH∥AD.
∵AD⊥AB,∴MH⊥AB.
分别以AB,MH,MC为x,y,z轴建立空间直角坐标系.(6分)
得B(
,0,0),H(0,
,0),C(0,0,
),
∴
=(-
,
,0),
=(-
,0,
).(8分)
设平面BCD的法向量为
=(x,y,z),
∴
?
?
=(1,
,1).(10分)
又∵平面ABD的法向量为
=(0,0,1),
∴cos<
,
>=
=
显然二面角C-BD-A为锐角,所以它的大小为60°.(12分)

 解:(I)∵DA=AC=1,DC=
解:(I)∵DA=AC=1,DC=| 2 |
∴AC2+AD2=CD2,∴DA⊥AC.(3分)
又∵DA⊥AB,∴AB∩AC=A∴DA⊥平面ABC.(6分)
(II)方法一:取AB中点M,连CM,
过M作MN⊥BD交BD于N,
连CN.∵CA=CB=1,∴CM⊥AB,
∵DA?平面ABD,DA⊥平面ABC,
∴平面ABC⊥平面ABD.(8分)
∴CM⊥平面ABD,∴CM⊥BD.
又∵MN⊥BD,MN∩CM=M
∴BD⊥平面CMN,
∴∠CNM为二面角C-BD-A的平面角.(10分)
∴MN=
| ||||
|
| ||
| 6 |
| ||
| 2 |
tan∠CNM=
| CM |
| MN |
| 3 |
故二面角C-BD-A平面角的度数为60°.(12分)
 方法二:取AB中点M,连CM.
方法二:取AB中点M,连CM.∵AC=AB=1,∴CM⊥AB.
又∵平面ABC⊥平面ABD,∴CM⊥平面ABD.
取BD中点H,∴MH∥AD.
∵AD⊥AB,∴MH⊥AB.
分别以AB,MH,MC为x,y,z轴建立空间直角坐标系.(6分)
得B(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| BH |
| ||
| 2 |
| 1 |
| 2 |
| BC |
| ||
| 2 |
| ||
| 2 |
设平面BCD的法向量为
| n |
∴
|
|
| n |
| 2 |
又∵平面ABD的法向量为
| m |
∴cos<
| n |
| m |
| ||||
|
|
| 1 |
| 2 |
显然二面角C-BD-A为锐角,所以它的大小为60°.(12分)

点评:本小题主要考查空间线面关系中的垂直关系:线面垂直的判定与性质定理的综合运用、二面角的度量:二面角的平面角的作法①三垂线法,②定义法,利用空间向量的知识解决几何中的量,考查空间想象能力、推理论证能力和运算求解能力

练习册系列答案
相关题目
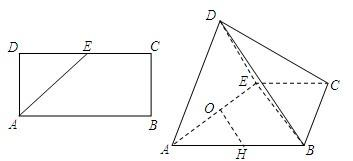 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2
 (2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使
(2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使