题目内容
已知:函数f(x)=ax2-2x+1.
(1)若 ≤a≤1,且f(x)在[1,3]上的最大值为M (a),最小值为N (a),令g(a)=M(a)-N (a),求g(a)的表达式;
≤a≤1,且f(x)在[1,3]上的最大值为M (a),最小值为N (a),令g(a)=M(a)-N (a),求g(a)的表达式;
(2)在(1)的条件下,求证:g(a)≥ ;
;
(3)设a>0,证明对任意的x1,x2∈[ ,+∞),|f(x1)-f(x2)|≥a(x1-x2).
,+∞),|f(x1)-f(x2)|≥a(x1-x2).
解:(1)∵f(x)=ax2-2x+1.
∴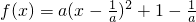 ,
,
由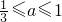 得
得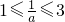 ,
,
∴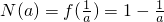 .
.
当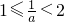 ,即
,即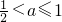 时,
时,
M(a)=f(3)=9a-5,
故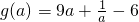 ;
;
当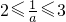 ,即
,即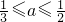 时,
时,
M(a)=f(1)=a-1,
故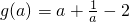 .
.
∴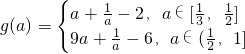 .
.
(2)∵当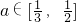 时,
时,
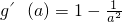 <0,
<0,
∴函数g(a)在 上为减函数;
上为减函数;
当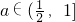 时,
时,
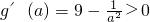 ,
,
∴函数g(a)在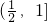 上为增函数,
上为增函数,
∴当 时,g(a)取最小值,
时,g(a)取最小值,
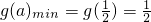 ,
,
故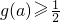 .
.
(3)∵当a>0时,抛物线f(x)=ax2-2x+1开口向上,
对称轴为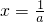 ,
,
∴函数f(x)在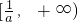 上为增函数,
上为增函数,
(或由f'(x)=2ax-2≥0得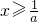 ,
,
∴函数f(x)在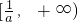 上为增函数,
上为增函数,
不妨设x1≤x2,由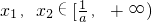 ,
,
得f(x1)≤f(x2)
∴|f(x1)-f(x2)|≥a|x1-x2|,
∴f(x2)-f(x1)≥a(x2-x1),
∴f(x2)-ax2≥f(x1)-ax1
令φ(x)=f(x)-ax=ax2-(a+2)x+1,x∈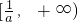
∵抛物线y=φ(x)开口向上,
对称轴为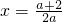 ,
,
且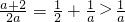 ,
,
∴函数φ(x)在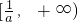 上单调递增,
上单调递增,
∴对任意的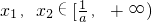 ,x2≥x1,
,x2≥x1,
有φ(x2)≥φ(x1),
即f(x2)-ax2≥f(x1)-ax1,
∴|f(x1)-f(x2)|≥a|x1-x2|.
分析:(1)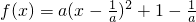 ,由
,由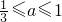 得
得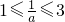 .所以
.所以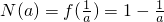 .当
.当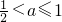 时,M(a)=f(3)=9a-5.当
时,M(a)=f(3)=9a-5.当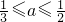 时,M(a)=f(1)=a-1,由此能求出g(a)的表达式.
时,M(a)=f(1)=a-1,由此能求出g(a)的表达式.
(2)当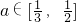 时,
时,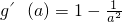 <0,所以函数g(a)在
<0,所以函数g(a)在 上为减函数;当
上为减函数;当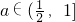 时,
时,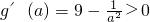 ,所以函数g(a)在
,所以函数g(a)在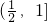 上为增函数,由此能够证明
上为增函数,由此能够证明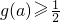 .
.
(3)当a>0时,抛物线f(x)=ax2-2x+1开口向上,对称轴为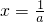 ,函数f(x)在
,函数f(x)在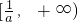 上为增函数;抛物线y=φ(x)开口向上,对称轴为
上为增函数;抛物线y=φ(x)开口向上,对称轴为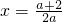 ,且
,且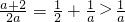 ,函数φ(x)在
,函数φ(x)在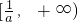 上单调递增.由此能够证明|f(x1)-f(x2)|≥a|x1-x2|.
上单调递增.由此能够证明|f(x1)-f(x2)|≥a|x1-x2|.
点评:本题考查二次函数性质的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,容易出易.解题时要认真审题,注意分类讨论思想的灵活运用.
∴
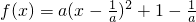 ,
,由
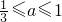 得
得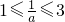 ,
,∴
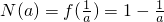 .
.当
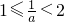 ,即
,即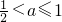 时,
时,M(a)=f(3)=9a-5,
故
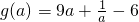 ;
;当
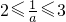 ,即
,即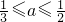 时,
时,M(a)=f(1)=a-1,
故
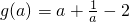 .
.∴
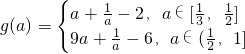 .
.(2)∵当
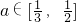 时,
时,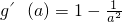 <0,
<0,∴函数g(a)在
 上为减函数;
上为减函数;当
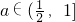 时,
时,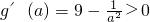 ,
,∴函数g(a)在
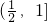 上为增函数,
上为增函数,∴当
 时,g(a)取最小值,
时,g(a)取最小值,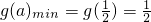 ,
,故
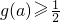 .
.(3)∵当a>0时,抛物线f(x)=ax2-2x+1开口向上,
对称轴为
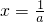 ,
,∴函数f(x)在
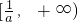 上为增函数,
上为增函数,(或由f'(x)=2ax-2≥0得
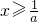 ,
,∴函数f(x)在
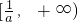 上为增函数,
上为增函数,不妨设x1≤x2,由
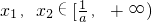 ,
,得f(x1)≤f(x2)
∴|f(x1)-f(x2)|≥a|x1-x2|,
∴f(x2)-f(x1)≥a(x2-x1),
∴f(x2)-ax2≥f(x1)-ax1
令φ(x)=f(x)-ax=ax2-(a+2)x+1,x∈
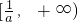
∵抛物线y=φ(x)开口向上,
对称轴为
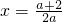 ,
,且
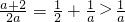 ,
,∴函数φ(x)在
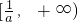 上单调递增,
上单调递增,∴对任意的
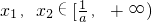 ,x2≥x1,
,x2≥x1,有φ(x2)≥φ(x1),
即f(x2)-ax2≥f(x1)-ax1,
∴|f(x1)-f(x2)|≥a|x1-x2|.
分析:(1)
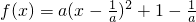 ,由
,由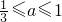 得
得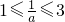 .所以
.所以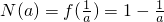 .当
.当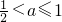 时,M(a)=f(3)=9a-5.当
时,M(a)=f(3)=9a-5.当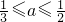 时,M(a)=f(1)=a-1,由此能求出g(a)的表达式.
时,M(a)=f(1)=a-1,由此能求出g(a)的表达式.(2)当
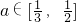 时,
时,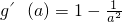 <0,所以函数g(a)在
<0,所以函数g(a)在 上为减函数;当
上为减函数;当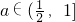 时,
时,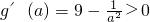 ,所以函数g(a)在
,所以函数g(a)在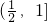 上为增函数,由此能够证明
上为增函数,由此能够证明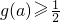 .
.(3)当a>0时,抛物线f(x)=ax2-2x+1开口向上,对称轴为
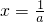 ,函数f(x)在
,函数f(x)在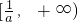 上为增函数;抛物线y=φ(x)开口向上,对称轴为
上为增函数;抛物线y=φ(x)开口向上,对称轴为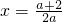 ,且
,且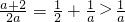 ,函数φ(x)在
,函数φ(x)在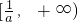 上单调递增.由此能够证明|f(x1)-f(x2)|≥a|x1-x2|.
上单调递增.由此能够证明|f(x1)-f(x2)|≥a|x1-x2|.点评:本题考查二次函数性质的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,容易出易.解题时要认真审题,注意分类讨论思想的灵活运用.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目