题目内容
已知函数f(x)=| A |
| 2 |
| A |
| 2 |
| π |
| 2 |
(1)求φ;
(2)计算f(1)+f(2)+…+f(2010);
(3)若函数g(x)=f(x)-m-1在区间[1,4]上恰有一个零点,求m的范围.
分析:(1)根据函数的周期求出ω的值,根据函数的最大值求出A的值,根据函数过点(1,2)及∅的范围求出∅的值.
(2)由(1)知f(x)=1-cos2(
x+
)且周期为4,2010=4×502+2,故 f(1)+f(2)+…+f(2010)=
f(1)+f(2).
(3)由g(x)=f(x)-m-1=-cos(
x+
)-m=sin
x-m在区间[1,4]上恰有一个零点知:函数y=sin
x的
图象与直线恰有一个交点.在同一直角坐标系内作出这两个函数的图象,结合图象可得m的取值范围.
(2)由(1)知f(x)=1-cos2(
| π |
| 4 |
| π |
| 4 |
f(1)+f(2).
(3)由g(x)=f(x)-m-1=-cos(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
图象与直线恰有一个交点.在同一直角坐标系内作出这两个函数的图象,结合图象可得m的取值范围.
解答:解:(1)∵
=2,T=4,ω>0∴2ω=
=
∴ω=
,由于f(x)的最大值为2且A>0,
所以
+
=2,即A=2,得 f(x)=1-cos2(
x+φ),又函数f(x)的图象过点(1,2)则cos2(
+φ)=-1∴sin2φ=1∴2φ=2kπ+
,φ=kπ+
∵0<φ<
∴φ=
.
(2)由(1)知f(x)=1-cos2(
x+
)且周期为4,2010=4×502+2,
∵f(1)=2,f(2)=1,f(3)=0,f(4)=1,∴f(1)+f(2)+f(3)+f(4)=4,
故 f(1)+f(2)+…+f(2010)=502×4+f(1)+f(2)=2008+3=2011.
(3)由g(x)=f(x)-m-1=-cos(
x+
)-m=sin
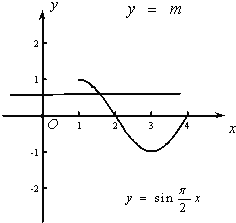
x-m在区间[1,4]上恰有一个零点知:
函数y=sin
x的图象与直线y=m恰有一个交点.在同一直角坐标系内作出这两个函数的图象(如图所示),
由图象可知 0<m≤1或 m=-1,故m的取值范围是{m|0<m≤1,或 m=-1}.
| T |
| 2 |
| 2π |
| T |
| π |
| 2 |
| π |
| 4 |
所以
| A |
| 2 |
| A |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
(2)由(1)知f(x)=1-cos2(
| π |
| 4 |
| π |
| 4 |
∵f(1)=2,f(2)=1,f(3)=0,f(4)=1,∴f(1)+f(2)+f(3)+f(4)=4,
故 f(1)+f(2)+…+f(2010)=502×4+f(1)+f(2)=2008+3=2011.
(3)由g(x)=f(x)-m-1=-cos(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
函数y=sin
| π |
| 2 |
由图象可知 0<m≤1或 m=-1,故m的取值范围是{m|0<m≤1,或 m=-1}.

点评:本题考查三角函数的最值,函数的零点,三角函数的周期性和求法,体现了数形结合的数学思想,求出函数f(x) 的
解析式,是解题的突破口.
解析式,是解题的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |