题目内容
(本题满分12分)
已知集合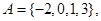 在平面直角坐标系中,点
在平面直角坐标系中,点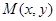 的横、纵坐标满足
的横、纵坐标满足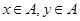 。
。
(1)请列出点 的所有坐标;
的所有坐标;
(2)求点 不在
不在 轴上的概率;
轴上的概率;
(3)求点 正好落在区域
正好落在区域 上的概率。
上的概率。
(1)(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)
(2) (3)
(3)
解析试题分析:(1) 集合
集合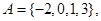 点
点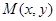 的横、纵坐标满足
的横、纵坐标满足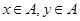 ,
, 点
点 的坐标共有:
的坐标共有: 个,分别是:
个,分别是:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)……4分
(2)点 不在
不在 轴上的坐标共有12种:
轴上的坐标共有12种:
(-2,-2),(0,-2),(-2,1),(-2,3);(1,-2),(0,1),(1,1),(1,3);
(3,-2),(0,3),(3,1),(3,3)
所以点 不在
不在 轴上的概率是
轴上的概率是 ……8分
……8分
(3)点 正好落在区域
正好落在区域 上的坐标共有3种:(1,1),(1,3),(3,1)
上的坐标共有3种:(1,1),(1,3),(3,1)
故 正好落在该区域上的概率为
正好落在该区域上的概率为 ……12分
……12分
考点:古典概型概率
点评:古典概率需要找到所有基本事件总数及满足某一条件的基本事件数目,然后求其比值

练习册系列答案
相关题目
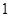 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率; 次,求在这三枪中出现空弹的概率
次,求在这三枪中出现空弹的概率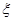 个球,求
个球,求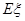 。
。 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响. ,求随即变量
,求随即变量 和
和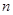 ,将
,将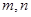 作为Q点的横、纵坐标,
作为Q点的横、纵坐标,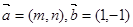 的夹角为
的夹角为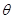 ,求
,求 的概率;
的概率;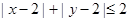 内的概率.
内的概率. 之间的均匀随机数
之间的均匀随机数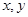 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.