题目内容
【题目】一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )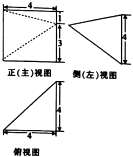
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
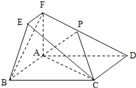
【解析】解:由三视图知:几何体是四棱锥,且四棱锥的一个侧面与底面垂直,
底面为边长为4的正方形如图:
其中PAD⊥平面ABCD,底面ABCD为正方形,
PE⊥AD,DE=1,AE=3,PE=4, ![]()
PE⊥底面ABCD,连接CE,BE,
在直角三角形PBE中,
PB= ![]() =
= ![]() =
= ![]() ;
;
在直角三角形PCE中,
可得PC= ![]() =
= ![]() =
= ![]() ;
;
又PA= ![]() =
= ![]() =5;
=5;
PD= ![]() =
= ![]() =
= ![]() .
.
几何体最长棱的棱长为 ![]() .
.
故选:C.
【考点精析】关于本题考查的由三视图求面积、体积,需要了解求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积才能得出正确答案.

练习册系列答案
相关题目