题目内容
在1和2之间依次插入n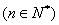 个正数
个正数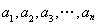 使得这
使得这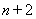 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这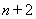 个数的乘积记作
个数的乘积记作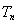 ,令
,令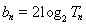 .
.
(1)求数列{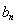 }的通项公式;
}的通项公式;
(2)令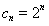 ,设
,设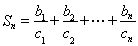 ,求
,求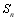 .
.
【答案】
(1)  ;(2)
;(2)  .
.
【解析】
试题分析:(1)由题意可设等比数列1,  ,2的公比为
,2的公比为 则
则 ,
, ;根据题意可知
;根据题意可知
 所以
所以 .
.
(2)由(1)和已知 得
得  ,
,
再由错位相减法求得: ,进而求出
,进而求出 .
.
试题解析:(1)法一:设等比数列1,  ,2的公比为
,2的公比为 则
则 ,
, ; 2分
; 2分
所以
 6分
6分

 7分
7分
(2)由已知 得
得  ,
,
由错位相减法求得: 10分
10分

 13分
13分
(1)法二:设等比数列1,  ,2的公比为
,2的公比为 ,
,
则 ,
, . ∴
. ∴ . 4分
. 4分


 ,
,  7分
7分
(1)法三:又

由等比数列的性质得: ∴
∴ 7分
7分
考点:1.等比数列的性质应用;2.错位相减法求数列前n项和.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目