题目内容
已知函数f(x)=|3x-2|+x
(1)求函数f(x)的值域;
(2)若g(x)=|x+1|,解不等式f(x)>g(x).
解:(1)由题意令3x-2=0,解得x= ,分两种情况:
,分两种情况:
当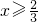 时,
时, ,
,
当 时,
时, ,
,
所以f(x)的值域为R;
(2)令x+1=0解得,x=-1,故分三种情况:
当x<-1时,原不等式等价于-3x+2+x>-1-x,解得x<-1,则解集为{x|x<-1};
当 时,原不等式等价于-3x+2+x>x+1,解得
时,原不等式等价于-3x+2+x>x+1,解得 ,则解集为{x|
,则解集为{x| };
};
当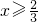 时,原不等式等价于3x-2+x>x+1,解得x>1,则解集为{x|x>1};
时,原不等式等价于3x-2+x>x+1,解得x>1,则解集为{x|x>1};
综上,不等式f(x)>g(x)的解集为 .
.
分析:(1)令3x-2=0求出x= ,故根据x与
,故根据x与 的大小关系,分两种情况去掉绝对值化简解析式,并求出在每个范围内的值域,最后并在一起;
的大小关系,分两种情况去掉绝对值化简解析式,并求出在每个范围内的值域,最后并在一起;
(2)令x+1=0得x=-1,由(1)故根据x与 、-1的大小关系,分三种情况去掉绝对值化简解析式,并求出在每个范围内的解集,最后并在一起.
、-1的大小关系,分三种情况去掉绝对值化简解析式,并求出在每个范围内的解集,最后并在一起.
点评:本题的考点是含有绝对值的函数问题,即根据绝对值中式子与零的关系,进行分类求解,最后结果要求并集.
 ,分两种情况:
,分两种情况:当
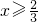 时,
时, ,
,当
 时,
时, ,
,所以f(x)的值域为R;
(2)令x+1=0解得,x=-1,故分三种情况:
当x<-1时,原不等式等价于-3x+2+x>-1-x,解得x<-1,则解集为{x|x<-1};
当
 时,原不等式等价于-3x+2+x>x+1,解得
时,原不等式等价于-3x+2+x>x+1,解得 ,则解集为{x|
,则解集为{x| };
};当
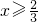 时,原不等式等价于3x-2+x>x+1,解得x>1,则解集为{x|x>1};
时,原不等式等价于3x-2+x>x+1,解得x>1,则解集为{x|x>1};综上,不等式f(x)>g(x)的解集为
 .
.分析:(1)令3x-2=0求出x=
 ,故根据x与
,故根据x与 的大小关系,分两种情况去掉绝对值化简解析式,并求出在每个范围内的值域,最后并在一起;
的大小关系,分两种情况去掉绝对值化简解析式,并求出在每个范围内的值域,最后并在一起;(2)令x+1=0得x=-1,由(1)故根据x与
 、-1的大小关系,分三种情况去掉绝对值化简解析式,并求出在每个范围内的解集,最后并在一起.
、-1的大小关系,分三种情况去掉绝对值化简解析式,并求出在每个范围内的解集,最后并在一起.点评:本题的考点是含有绝对值的函数问题,即根据绝对值中式子与零的关系,进行分类求解,最后结果要求并集.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|