题目内容
1.某学校开设A类选修课3门,B类选修课4门,一位同学从中一共选3门,要求两类课必须选一门,则不同选法共( )| A. | 30种 | B. | 35种 | C. | 42种 | D. | 48种 |
分析 根据题意,要求两类课程中各至少选一门,分两种情况讨论:①A类选修课选1门,B类选修课选2门;②A类选修课选2门,B类选修课选1门;由组合数公式求出每种情况的选法数目,根据分类计数原理得到结果.
解答 解:可分以下2种情况:①A类选修课选1门,B类选修课选2门,有C31C42种不同的选法;
②A类选修课选2门,B类选修课选1门,有C32C41种不同的选法.
∴根据分类计数原理知不同的选法共有C31C42+C32C41=18+12=30种.
故要求两类课程中各至少选一门,则不同的选法共有30种.
故选:A.
点评 本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想,解答的关键是根据题意确定分类讨论的依据,做到不重不漏.

练习册系列答案
相关题目
11.铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),求购买铁矿石的最少费用.
| a | b(万吨) | c(百万元) | |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
12.使cosx=1-m有意义的m的取值范围为( )
| A. | m≥0 | B. | 0≤m≤2 | C. | -1<m<1 | D. | m<-1或m>1 |
6.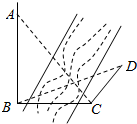 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
7.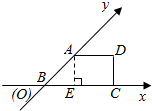 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )| A. | 2+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
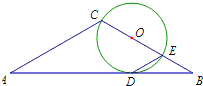 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.