题目内容
19.某三棱锥的三视图如图所示,该三棱锥的四个面的面积中,最大的是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{7}$ | D. | $2\sqrt{3}$ |
分析 三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,先确定最大的面,再求其面积.
解答 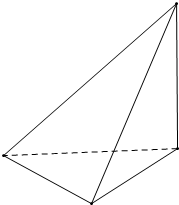 解:由三视图可知,该几何体有两个面是直角三角形,如右图,
解:由三视图可知,该几何体有两个面是直角三角形,如右图,
底面是正三角形,
最大的面是第四个面,
其边长分别为:
2,$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
故其面积为:
$\frac{1}{2}$×2×$\sqrt{8-1}$=$\sqrt{7}$;
故选C.
点评 三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
12. 已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )
已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )
 已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )
已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )| A. | 8 | B. | 8$\sqrt{3}$ | C. | 16 | D. | 16$\sqrt{3}$ |