题目内容
已知函数f(x)=ax2-4bx+2alnx(a,b∈R)
(I)若函数y=f(x)存在极大值和极小值,求 的取值范围;
的取值范围;
(II)设m,n分别为f(x)的极大值和极小值,若存在实数,b∈(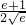 a,
a,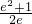 a),使得m-n=1,求a的取值范围.(e为自然对数的底)
a),使得m-n=1,求a的取值范围.(e为自然对数的底)
解:(I)f′(x)=2ax-4b+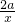 =
=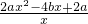 ,其中x>0,
,其中x>0,
由于函数y=f(x)存在极大值和极小值,
故方程f′(x)=0有两个不等的正实数根,即2ax2-4bx+2a=0有两个不等的正实数根,记为x1,x2,显然a≠0,
所以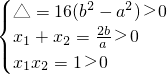 ,解得
,解得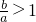 ;
;
(II)由b∈(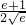 a,
a,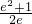 a)得a>0,且
a)得a>0,且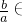 (
(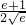 ,
,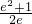 ),
),
由(I)知f(x)存在极大值和极小值,
设f′(x)=0的两根为x1,x2(0<x1<x2),则f(x)在(0,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增,
所以m=f(x1),n=f(x2),
因为x1x2=1,所以0<x1<1<x2,而且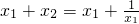 =
=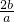 ∈(
∈(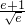 ,
, ),
),
由于函数y=x+ 在(0,1)上递减,所以
在(0,1)上递减,所以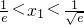 ,
,
又由于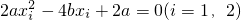 ,
,
所以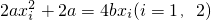 ,
,
所以m-n=f(x1)-f(x2)
=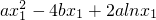 -
-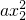 +4bx2-2alnx2
+4bx2-2alnx2
= +2a(lnx1-lnx2)
+2a(lnx1-lnx2)
=-a(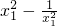 )+2aln
)+2aln ,
,
令t= ,则m-n=-a(t-
,则m-n=-a(t- )+2alnt,令h(t)=-(t-
)+2alnt,令h(t)=-(t- )+2lnt(
)+2lnt(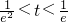 ),
),
所以h′(t)=-1- +
+ =-
=-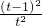 ≤0,所以h(t)在(
≤0,所以h(t)在(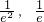 )上单调递减,所以e-e-1-2<h(t)<e2-e-2-4,
)上单调递减,所以e-e-1-2<h(t)<e2-e-2-4,
由m-n=ah(t)=1,知a=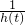 ,所以
,所以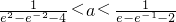 .
.
分析:(I)由于定义域为(0,+∞)且y=f(x)存在极大值、极小值,所以f′(x)=0有两个不等的正实数根,从而可转化为二次方程根的分布问题,借助判别式、韦达定理可得不等式组,由此可得 的取值范围;
的取值范围;
(II)由b∈(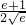 a,
a,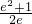 a)得a>0,且
a)得a>0,且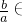 (
(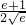 ,
,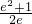 ),由(I)知f(x)存在极大值和极小值,设f′(x)=0的两根为x1,x2(0<x1<x2),则f(x)在(0,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增,所以m=f(x1),n=f(x2),根据x1x2=1可把m-n表示为关于x1,a的表达式,且表达式为1,借助x1范围可得a的范围;
),由(I)知f(x)存在极大值和极小值,设f′(x)=0的两根为x1,x2(0<x1<x2),则f(x)在(0,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增,所以m=f(x1),n=f(x2),根据x1x2=1可把m-n表示为关于x1,a的表达式,且表达式为1,借助x1范围可得a的范围;
点评:本题考查利用导数研究函数的极值及函数的单调性,考查学生综合运用知识分析问题解决问题的能力,本题综合性强、计算量大,能力要求高.
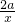 =
=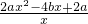 ,其中x>0,
,其中x>0,由于函数y=f(x)存在极大值和极小值,
故方程f′(x)=0有两个不等的正实数根,即2ax2-4bx+2a=0有两个不等的正实数根,记为x1,x2,显然a≠0,
所以
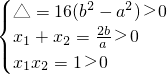 ,解得
,解得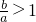 ;
;(II)由b∈(
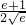 a,
a,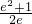 a)得a>0,且
a)得a>0,且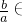 (
(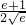 ,
,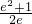 ),
),由(I)知f(x)存在极大值和极小值,
设f′(x)=0的两根为x1,x2(0<x1<x2),则f(x)在(0,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增,
所以m=f(x1),n=f(x2),
因为x1x2=1,所以0<x1<1<x2,而且
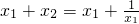 =
=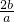 ∈(
∈(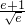 ,
, ),
),由于函数y=x+
 在(0,1)上递减,所以
在(0,1)上递减,所以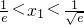 ,
,又由于
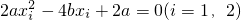 ,
,所以
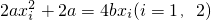 ,
,所以m-n=f(x1)-f(x2)
=
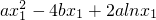 -
-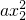 +4bx2-2alnx2
+4bx2-2alnx2=
 +2a(lnx1-lnx2)
+2a(lnx1-lnx2)=-a(
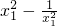 )+2aln
)+2aln ,
,令t=
 ,则m-n=-a(t-
,则m-n=-a(t- )+2alnt,令h(t)=-(t-
)+2alnt,令h(t)=-(t- )+2lnt(
)+2lnt(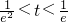 ),
),所以h′(t)=-1-
 +
+ =-
=-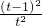 ≤0,所以h(t)在(
≤0,所以h(t)在(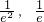 )上单调递减,所以e-e-1-2<h(t)<e2-e-2-4,
)上单调递减,所以e-e-1-2<h(t)<e2-e-2-4,由m-n=ah(t)=1,知a=
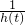 ,所以
,所以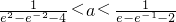 .
.分析:(I)由于定义域为(0,+∞)且y=f(x)存在极大值、极小值,所以f′(x)=0有两个不等的正实数根,从而可转化为二次方程根的分布问题,借助判别式、韦达定理可得不等式组,由此可得
 的取值范围;
的取值范围;(II)由b∈(
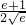 a,
a,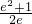 a)得a>0,且
a)得a>0,且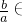 (
(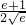 ,
,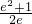 ),由(I)知f(x)存在极大值和极小值,设f′(x)=0的两根为x1,x2(0<x1<x2),则f(x)在(0,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增,所以m=f(x1),n=f(x2),根据x1x2=1可把m-n表示为关于x1,a的表达式,且表达式为1,借助x1范围可得a的范围;
),由(I)知f(x)存在极大值和极小值,设f′(x)=0的两根为x1,x2(0<x1<x2),则f(x)在(0,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增,所以m=f(x1),n=f(x2),根据x1x2=1可把m-n表示为关于x1,a的表达式,且表达式为1,借助x1范围可得a的范围;点评:本题考查利用导数研究函数的极值及函数的单调性,考查学生综合运用知识分析问题解决问题的能力,本题综合性强、计算量大,能力要求高.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目