题目内容
若函数f(x)=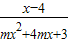 的定义域为R,则实数m的取值范围是 .
的定义域为R,则实数m的取值范围是 .
【答案】分析:从函数解析式的结构来看,要使其有意义需满足mx2+4mx+3≠0,所以由题意将所给条件转化为mx2+4mx+3≠0对任意x∈R恒成立,再进行分类讨论求解.
解答:解:由题意知mx2+4mx+3≠0对任意x∈R恒成立,
(1)若m=0,则mx2+4mx+3=3≠0,符合题意.
(2)若m≠0,则mx2+4mx+3≠0对任意x∈R恒成立,等价于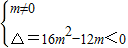 ,
,
解得: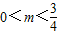 ,
,
综上所述,实数m的取值范围是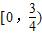 .
.
故答案为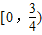 .
.
点评:此题表面看是研究函数的定义域,实则是一个恒成立问题,转化题意后因为最早次幂位置有参数,所以要进行分类讨论,此处为易错点.
解答:解:由题意知mx2+4mx+3≠0对任意x∈R恒成立,
(1)若m=0,则mx2+4mx+3=3≠0,符合题意.
(2)若m≠0,则mx2+4mx+3≠0对任意x∈R恒成立,等价于
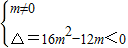 ,
,解得:
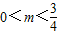 ,
,综上所述,实数m的取值范围是
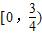 .
.故答案为
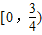 .
.点评:此题表面看是研究函数的定义域,实则是一个恒成立问题,转化题意后因为最早次幂位置有参数,所以要进行分类讨论,此处为易错点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. .
. 与
与 的大小,并说明你的理由.
的大小,并说明你的理由. .
. .
. 与
与 的大小,并说明你的理由.
的大小,并说明你的理由. .
. .
. 与
与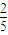 的大小,并说明你的理由.
的大小,并说明你的理由.