题目内容
若函数f(x)=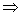
是奇函数,则a+b=______________.
1 f(0)=a=0.当x＞0时,-x＜0,f(-x)=-x+b,f(x)=x-1.f(-x)=-f(x),即-x+b=1-xb=1.
∴a+b=1.
练习册系列答案
相关题目
是奇函数,则a+b=______________.题目内容
若函数f(x)=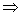是奇函数,则a+b=______________.
1 f(0)=a=0.当x＞0时,-x＜0,f(-x)=-x+b,f(x)=x-1.f(-x)=-f(x),即-x+b=1-xb=1.
∴a+b=1.
是奇函数，则m的值是：
是奇函数，则a＋b＝________．
)是奇函数，则a=________________.
是奇函数．
的单调增区间是（－∞，0）
（0，+∞）