题目内容
已知圆C的方程为x2+y2=4,过点M(2,4)作圆C的两条切线,切点分别为A,B,直线AB恰好经过椭圆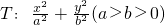 的右顶点和上顶点.
的右顶点和上顶点.
(1)求椭圆T的方程;
(2)是否存在斜率为 的直线l与曲线C交于P、Q两不同点,使得
的直线l与曲线C交于P、Q两不同点,使得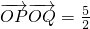 (O为坐标原点),若存在,求出直线l的方程,否则,说明理由.
(O为坐标原点),若存在,求出直线l的方程,否则,说明理由.
解:(1)由题意:一条切线方程为:x=2,
设另一条切线方程为:y-4=k(x-2).(2分)
则: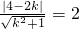 ,
,
解得: ,此时切线方程为:
,此时切线方程为: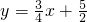
切线方程与圆方程联立得: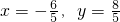 ,
,
则直线AB的方程为x+2y=2.(4分)
令x=0,解得y=1,∴b=1;
令y=0,得x=2,∴a=2
故所求椭圆方程为 .(6分)
.(6分)
(2)设存在直线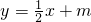 满足题意,
满足题意,
联立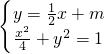
整理得x2+2mx+2m2-2=0,
令P(x1,y1),Q(x2,y2),则
∴x1+x2=-2m, ,
,
△=(2m)2-8(m2-1)>0,即m2<2.(8分)
由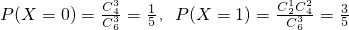 ,
,
得:x1x2+y1y2=0,

=
所以, 不满足m2<2.(10分)
不满足m2<2.(10分)
因此不存在直线满足题意.(12分)
分析:(1)先由题意求出切线方程,把切线方程与圆方程联立,求出直线AB的方程,由此能够求出椭圆方程.
(2)设存在直线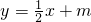 满足题意,与椭圆联立,得x2+2mx+2m2-2=0,令P(x1,y1),Q(x2,y2),利用韦达定理和根的判别式结合题设条件得到不存在直线满足题意.
满足题意,与椭圆联立,得x2+2mx+2m2-2=0,令P(x1,y1),Q(x2,y2),利用韦达定理和根的判别式结合题设条件得到不存在直线满足题意.
点评:本题考查椭圆方程的求法,探索直线方程是否存在.解题时要认真审题,仔细解答,注意直线方程的求法和合理运用.
设另一条切线方程为:y-4=k(x-2).(2分)
则:
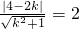 ,
,解得:
 ,此时切线方程为:
,此时切线方程为: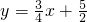
切线方程与圆方程联立得:
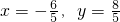 ,
,则直线AB的方程为x+2y=2.(4分)
令x=0,解得y=1,∴b=1;
令y=0,得x=2,∴a=2
故所求椭圆方程为
 .(6分)
.(6分)(2)设存在直线
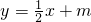 满足题意,
满足题意,联立
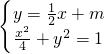
整理得x2+2mx+2m2-2=0,
令P(x1,y1),Q(x2,y2),则
∴x1+x2=-2m,
 ,
,△=(2m)2-8(m2-1)>0,即m2<2.(8分)
由
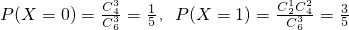 ,
,得:x1x2+y1y2=0,

=

所以,
 不满足m2<2.(10分)
不满足m2<2.(10分)因此不存在直线满足题意.(12分)
分析:(1)先由题意求出切线方程,把切线方程与圆方程联立,求出直线AB的方程,由此能够求出椭圆方程.
(2)设存在直线
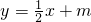 满足题意,与椭圆联立,得x2+2mx+2m2-2=0,令P(x1,y1),Q(x2,y2),利用韦达定理和根的判别式结合题设条件得到不存在直线满足题意.
满足题意,与椭圆联立,得x2+2mx+2m2-2=0,令P(x1,y1),Q(x2,y2),利用韦达定理和根的判别式结合题设条件得到不存在直线满足题意.点评:本题考查椭圆方程的求法,探索直线方程是否存在.解题时要认真审题,仔细解答,注意直线方程的求法和合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目