题目内容
等比数列{an}的公比q>1, ,
, ,则a3+a4+a5+a6+a7+a8等于( )
,则a3+a4+a5+a6+a7+a8等于( )
| A.64 | B.31 | C.32 | D.63 |
D
解析试题分析:因为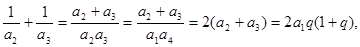 所以
所以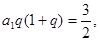 而
而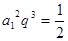 ,两式消去
,两式消去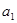 得
得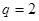 或
或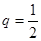 (舍),从而
(舍),从而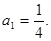 所求的和为
所求的和为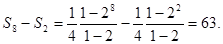 选D.
选D.
考点:等比数列的性质,等比数列求和

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
设等比数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,则
,则 ( )
( )
| A.60 | B.70 | C.90 | D.40 |
设数列 ,以下说法正确的是( )
,以下说法正确的是( )
A.若 , , ,则 ,则 为等比数列 为等比数列 |
B.若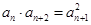 , , ,则 ,则 为等比数列 为等比数列 |
C.若 , , ,则 ,则 为等比数列 为等比数列 |
D.若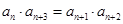 , , ,则 ,则 为等比数列 为等比数列 |
设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 的值为( )
的值为( )
A. | B. | C. | D.1 |
已知等比数列 中,
中, =1,
=1, =2,则
=2,则 等于( ).
等于( ).
| A.2 | B.2 | C.4 | D.4 |
正项等比数列 中,若
中,若 ,则
,则 等于( )
等于( )
| A.-16 | B.10 | C.16 | D.256 |
一个等比数列的第3项和第4项分别是12和18,则它的第2项为( )
| A.4 | B.8 | C. | D. |
如果数列a1, ,
, ,…,
,…, ,…是首项为1,公比为-
,…是首项为1,公比为- 的等比数列,那么a5等于( )
的等比数列,那么a5等于( )
| A.32 | B.64 |
| C.-32 | D.-64 |
 的前5项和为( )
的前5项和为( )


