题目内容
(12分)(2011•重庆)如图,椭圆的中心为原点0,离心率e=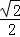 ,一条准线的方程是x=2
,一条准线的方程是x=2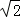
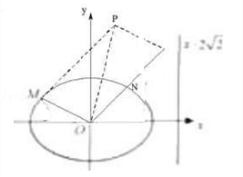
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点P满足: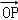 =
=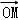 +2
+2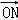 ,其中M、N是椭圆上的点,直线OM与ON的斜率之积为﹣
,其中M、N是椭圆上的点,直线OM与ON的斜率之积为﹣ ,
,
问:是否存在定点F,使得|PF|与点P到直线l:x=2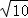 的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.
的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.
(Ⅰ)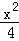 +
+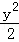 =1(Ⅱ)见解析
=1(Ⅱ)见解析
解析试题分析:(Ⅰ) 由题意得 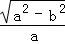 =
=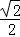 ,
,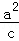 =
=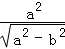 =2
=2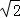 ,解出a、b 的值,即得椭圆的标准方程.
,解出a、b 的值,即得椭圆的标准方程.
(Ⅱ)设动点P(x,y),M(x1,y1)、N(x2,y2). 由向量间的关系得到 x=x1+2x2,y=y1+2y2,据
M、N是椭圆上的点可得 x2+2y2=20+4(x1x2+2y1y2).再根据直线OM与ON的斜率之积为﹣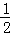 ,得到点P是椭圆
,得到点P是椭圆
x2+2y2="20" 上的点,根据椭圆的第二定义,存在点F(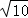 ,0),满足条件.
,0),满足条件.
解:(Ⅰ) 由题意得 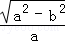 =
=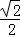 ,
,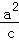 =
=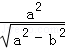 =2
=2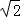 ,∴a=2,b=
,∴a=2,b=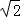 ,
,
故椭圆的标准方程为 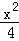 +
+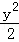 =1.
=1.
(Ⅱ)设动点P(x,y),M(x1,y1)、N(x2,y2).∵动点P满足: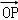 =
=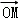 +2
+2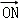 ,
,
∴(x,y)=(x1+2x2,y1+2y2 ),∴x=x1+2x2,y=y1+2y2,
∵M、N是椭圆上的点,∴x12+2y12﹣4=0,x22+2y22﹣4=0.
∴x2+2y2=(x1+2x2)2+2 (y1+2y2)2=(x12+2y12)+4(x22+2y22)+4(x1x2+2y1y2)
=4+4×4+4(x1x2+2y1y2)=20+4(x1x2+2y1y2).
∵直线OM与ON的斜率之积为﹣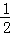 ,∴
,∴ •
•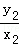 =﹣
=﹣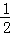 ,∴x2+2y2=20,
,∴x2+2y2=20,
故点P是椭圆 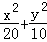 ="1" 上的点,焦点F(
="1" 上的点,焦点F(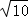 ,0),准线l:x=2
,0),准线l:x=2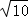 ,离心率为
,离心率为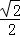 ,
,
根据椭圆的第二定义,|PF|与点P到直线l:x=2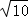 的距离之比为定值
的距离之比为定值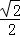 ,
,
故存在点F(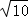 ,0),满足|PF|与点P到直线l:x=2
,0),满足|PF|与点P到直线l:x=2 的距离之比为定值.
的距离之比为定值.
点评:本题考查用待定系数法求椭圆的标准方程,两个向量坐标形式的运算,以及椭圆的第二定义,属于中档题.

 小夫子全能检测系列答案
小夫子全能检测系列答案 ,
, 的中点为
的中点为 ,动点
,动点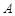 满足
满足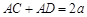 (
(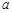 为正常数).
为正常数).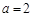 ,动点
,动点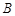 满足
满足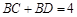 ,且
,且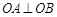 ,试求
,试求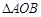 面积的最大值和最小值.
面积的最大值和最小值. :
: .
.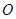 为原点,若点
为原点,若点 在椭圆
在椭圆 在直线
在直线 上,且
上,且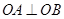 ,试判断直线
,试判断直线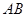 与圆
与圆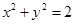 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.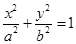 上的点M与椭圆右焦点
上的点M与椭圆右焦点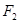 的连线
的连线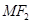 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.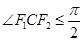 ;
;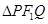 的面积是20
的面积是20 ,求此时椭圆的方程.
,求此时椭圆的方程.
 的圆心在坐标原点
的圆心在坐标原点 ,且恰好与直线
,且恰好与直线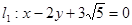 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,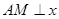 轴于点
轴于点 ,且动点
,且动点 满足
满足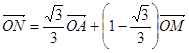 ,设动点
,设动点
 是椭圆
是椭圆 上任一点,点
上任一点,点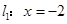 的距离为
的距离为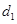 ,到点
,到点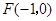 的距离为
的距离为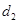 ,且
,且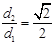 .直线
.直线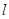 与椭圆
与椭圆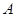 、
、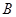 (
(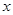 轴上方),且
轴上方),且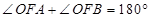 .
.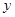 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线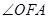 如何变化,直线
如何变化,直线
 :
: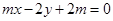
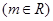 和椭圆
和椭圆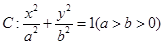 ,椭圆C的离心率为
,椭圆C的离心率为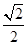 ,连结椭圆的四个顶点形成四边形的面积为
,连结椭圆的四个顶点形成四边形的面积为 .
.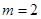 时,设直线
时,设直线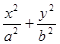 =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为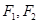 ,
,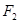 恰是抛物线C2:
恰是抛物线C2: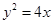 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|=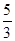 .
.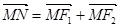 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若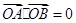 ,求直线l的方程.
,求直线l的方程.