题目内容
设函数 的定义域为集合A,关于x的不等式lg(2ax)<lg(a+x)(a>0)的解集为B,若A∩B=A,求实数a的取值范围.
的定义域为集合A,关于x的不等式lg(2ax)<lg(a+x)(a>0)的解集为B,若A∩B=A,求实数a的取值范围.
【答案】分析:通过求解函数的定义域求出集合A,利用对数函数的单调性,通过A∩B=A,得到a的关系式,求出a的范围.
解答:解:因为函数 的定义域为集合A,所以A={x|1<x≤2},
的定义域为集合A,所以A={x|1<x≤2},
当A∩B=A,即当1<x≤2时,关于x的不等式lg(2ax)<lg(a+x)(a>0)恒成立.
由2ax<a+x得a(2x-1)>0.
因为2x-1>0,所以a ,
,
又因为 的最小值为
的最小值为 ,
,
所以0<a< .
.
点评:本题考查函数的定义域的求法,分式不等式的解法,指数函数的单调性的应用,考查分析问题解决问题的能力.
解答:解:因为函数
 的定义域为集合A,所以A={x|1<x≤2},
的定义域为集合A,所以A={x|1<x≤2},当A∩B=A,即当1<x≤2时,关于x的不等式lg(2ax)<lg(a+x)(a>0)恒成立.
由2ax<a+x得a(2x-1)>0.
因为2x-1>0,所以a
 ,
,又因为
 的最小值为
的最小值为 ,
,所以0<a<
 .
.点评:本题考查函数的定义域的求法,分式不等式的解法,指数函数的单调性的应用,考查分析问题解决问题的能力.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
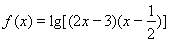

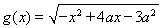
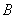
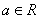
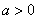

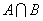
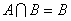
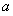
 .
. 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围. 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。 ,求实数
,求实数 的取值范围。
的取值范围。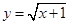 的定义域为集合
的定义域为集合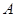 ,不等式
,不等式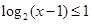 的解集为集合
的解集为集合 .
.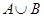 ,
, .
.