题目内容
已知函数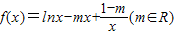
(1)当m=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当
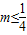 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;(3)设g(x)=x2-2x+n.当
 时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数n的取值范围.
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数n的取值范围.
【答案】分析:(1)欲求曲线y=f(x)在点(1,f(1))处的切线方程只需求出切线斜率k=f′(1),从而求出所求;
(2)先求导函数,然后讨论m的范围,得到导函数的符号,得到函数的单调性;
(3)根据(2)求出对任意x1∈(0,2),f(x1)≥f(1)= ,然后根据题意可知存在x2∈[1,2]使g(x)=x2-2x+n≤
,然后根据题意可知存在x2∈[1,2]使g(x)=x2-2x+n≤ ,解之即可.
,解之即可.
解答:解:(1)当m=2时,f(x)=lnx-2x- (x∈(0,+∞))
(x∈(0,+∞))
因此f(1)=-3,f′(x)= -2+
-2+ ,切线斜率k=f′(1)=0
,切线斜率k=f′(1)=0
所以切线方程为y=-3
(2)f′(x)= -m+
-m+ =
=
令h(x)=-mx2+x+m-1(x∈(0,+∞))
当m=0时,h(x)=x-1,令h(x)>0,x>1,h(x)<0,0<x<1
∴f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
当m≠0时,h(x)=-m(x-1)[x-( -1)],
-1)],
当m<0时, -1<0<1,f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
-1<0<1,f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
0<m≤ 时,0<1<
时,0<1< -1,f(x)在(0,1),(
-1,f(x)在(0,1),( -1,+∞)上是减函数,f(x)在(1,
-1,+∞)上是减函数,f(x)在(1, -1)上是增函数
-1)上是增函数
(3)当 时,f(x)在(0,1)上是减函数,f(x)在(1,2)上是增函数
时,f(x)在(0,1)上是减函数,f(x)在(1,2)上是增函数
∴对任意x1∈(0,2),f(x1)≥f(1)=
又已知存在x2∈[1,2],使f(x1)≥g(x2),
所以g(x2)≤ ,x2∈[1,2],
,x2∈[1,2],
即存在x2∈[1,2]使g(x)=x2-2x+n≤
即n-1≤ 解得n≤
解得n≤
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的单调性,同时考查了分类讨论的数学思想和转化的思想,属于中档题.
(2)先求导函数,然后讨论m的范围,得到导函数的符号,得到函数的单调性;
(3)根据(2)求出对任意x1∈(0,2),f(x1)≥f(1)=
 ,然后根据题意可知存在x2∈[1,2]使g(x)=x2-2x+n≤
,然后根据题意可知存在x2∈[1,2]使g(x)=x2-2x+n≤ ,解之即可.
,解之即可.解答:解:(1)当m=2时,f(x)=lnx-2x-
 (x∈(0,+∞))
(x∈(0,+∞))因此f(1)=-3,f′(x)=
 -2+
-2+ ,切线斜率k=f′(1)=0
,切线斜率k=f′(1)=0所以切线方程为y=-3
(2)f′(x)=
 -m+
-m+ =
=
令h(x)=-mx2+x+m-1(x∈(0,+∞))
当m=0时,h(x)=x-1,令h(x)>0,x>1,h(x)<0,0<x<1
∴f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
当m≠0时,h(x)=-m(x-1)[x-(
 -1)],
-1)],当m<0时,
 -1<0<1,f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数
-1<0<1,f(x)在(0,1)上是减函数,f(x)在(1,+∞)上是增函数0<m≤
 时,0<1<
时,0<1< -1,f(x)在(0,1),(
-1,f(x)在(0,1),( -1,+∞)上是减函数,f(x)在(1,
-1,+∞)上是减函数,f(x)在(1, -1)上是增函数
-1)上是增函数(3)当
 时,f(x)在(0,1)上是减函数,f(x)在(1,2)上是增函数
时,f(x)在(0,1)上是减函数,f(x)在(1,2)上是增函数∴对任意x1∈(0,2),f(x1)≥f(1)=

又已知存在x2∈[1,2],使f(x1)≥g(x2),
所以g(x2)≤
 ,x2∈[1,2],
,x2∈[1,2],即存在x2∈[1,2]使g(x)=x2-2x+n≤

即n-1≤
 解得n≤
解得n≤
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的单调性,同时考查了分类讨论的数学思想和转化的思想,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
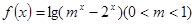
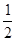 时,求f(x)的定义域
时,求f(x)的定义域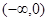 上的单调性并给出证明。
上的单调性并给出证明。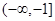 上恒取正值,求m的取值范围。
上恒取正值,求m的取值范围。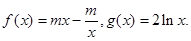
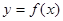 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;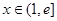 时,不等式
时,不等式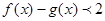 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
 存在两个零点,求m的取值范围;
存在两个零点,求m的取值范围; 。
。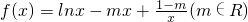
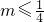 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;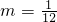 时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数n的取值范围.
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数n的取值范围.