题目内容
过点A(0,3),被圆(x-1)2+y2=4截得的弦长为2的直线方程是( )
A.y=-  x+3 x+3 | B.x=0或y=-  x+3 x+3 |
| C.x=0或y= x-3 | D.x=0 |
B
由圆的方程(x-1)2+y2=4,得:圆的圆心坐标为(1,0),半径为2。
令弦为AB、圆心为C、AB的中点为D。则有:CD⊥AD、AC=2、AD=√3,∴CD=1。
1、当要求的直线与x轴垂直时,直线方程就是:x=0。
显然,点C(1,0)到x=0的距离=1。
∴x=0是要求的一条直线。
2、当要求的直线存在斜率时,设要求直线的斜率为k。
则直线方程为:y-3=kx,即:kx-y+3=0。
而CD=|k-0+3|/√(k2+1),∴|k-0+3|/√(k2+1)=1,
∴|k+3|=√(k2+1),∴k2+6k+9=k2+1,∴6k=-8,∴k=-4/3。
∴此时要求的直线为:-(4/3)x-y+3=0,即:y =-(4/3)x+3。
综上所述,满足条件的直线方程是:x=0,或y =-(4/3)x+3。故选B。

练习册系列答案
相关题目
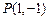 有一条直线l,它夹在两条直线
有一条直线l,它夹在两条直线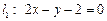 与
与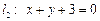 之间的线段恰被点P平分,求直线l的方程.
之间的线段恰被点P平分,求直线l的方程.  关于直线
关于直线 对称的直线方程是( ).
对称的直线方程是( ).



 、
、 和动点
和动点 满足:
满足: , 且存在正常数
, 且存在正常数 ,使得
,使得
 的方程;
的方程; 与曲线
与曲线 、
、 ,且与
,且与 轴的交点为
轴的交点为 .若
.若 求
求 与
与 垂直,则
垂直,则 ______.
______. 在第一象限上有一点
在第一象限上有一点 到
到 的距离为
的距离为 ,则点
,则点



 经过点
经过点 ,且在
,且在 轴、
轴、 轴上的截距互为相反数,则直线
轴上的截距互为相反数,则直线 经过点
经过点 ,且在
,且在 轴,
轴, 轴上的截距互为相反数,则直线
轴上的截距互为相反数,则直线