题目内容
【题目】已知函数
， 
，记
。
(1) 判断的奇偶性（不用证明）并写出的单调区间；
（2）若
对于一切
恒成立，求实数
的取值范围.
（3）对任意
，都存在
，使得
， 
.若
，求实数
的值；
【答案】（1）奇函数，在R上单调递增（2）
（3）
【解析】试题分析：（1）利用奇偶性的定义判断函数的奇偶性，利用复合函数的单调性性质写出单调区间；（2）含参数的恒成立问题采用分离参数法，得到
，解得
， 
的最大值，则
即可；（3）由题意可知， 
， 
，所以
，解得
。
试题解析：
（Ⅰ）函数
为奇函数，在R上单调递增
（Ⅱ）当
时， 
即
，
， 
令
， 
下面求函数
的最大值。
， 
∴
故
的取值范围是
（Ⅲ）据题意知，当
时， 
， 
∵
在区间
上单调递增，
∴
，即
又∵
∴函数
的对称轴为
∴函数
在区间
上单调递减
∴
，即
由
，得
，
∴
练习册系列答案
相关题目
【题目】某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
，
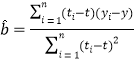