题目内容
已知 ,其中A,B,C是△ABC的内角.
,其中A,B,C是△ABC的内角.
(1)当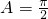 时,求
时,求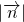 的值
的值
(2)若 ,当
,当 取最大值时,求A大小及AC边长.
取最大值时,求A大小及AC边长.
解:(1)当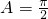 时,
时, =
= =
= .
.
∴ =
= .
.
(2)∵ =
= =
= =2
=2 +
+ .
.
∵0<A<π,∴ .
.
∴当 时,即A=
时,即A= 时,
时, ,此时
,此时 取得最大值2+
取得最大值2+ .
.
由余弦定理得BC2=AB2+AC2-2AB×ACcosA,即 ,
,
化为AC2-3AC+2=0,解得AC=1或2.
分析:(1)先化简 ,再利用模的计算公式即可得出;
,再利用模的计算公式即可得出;
(2)利用数量积的运算性质、倍角公式、诱导公式、两角和差的正弦公式即可得到A,再利用余弦定理即可得到AC.
点评:熟练掌握模的计算公式、数量积的运算性质、倍角公式、诱导公式、两角和差的正弦公式、余弦定理是解题的关键.
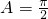 时,
时, =
= =
= .
.∴
 =
= .
.(2)∵
 =
= =
= =2
=2 +
+ .
.∵0<A<π,∴
 .
.∴当
 时,即A=
时,即A= 时,
时, ,此时
,此时 取得最大值2+
取得最大值2+ .
.由余弦定理得BC2=AB2+AC2-2AB×ACcosA,即
 ,
,化为AC2-3AC+2=0,解得AC=1或2.
分析:(1)先化简
 ,再利用模的计算公式即可得出;
,再利用模的计算公式即可得出;(2)利用数量积的运算性质、倍角公式、诱导公式、两角和差的正弦公式即可得到A,再利用余弦定理即可得到AC.
点评:熟练掌握模的计算公式、数量积的运算性质、倍角公式、诱导公式、两角和差的正弦公式、余弦定理是解题的关键.

练习册系列答案
相关题目
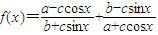 ,其中a、b、c为正实数,
,其中a、b、c为正实数,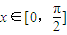 .
. ,其中A、B、C三点共线,则满足条件的x(
)
,其中A、B、C三点共线,则满足条件的x(
)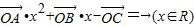 ,其中A、B、C三点共线,则满足条件的x( )
,其中A、B、C三点共线,则满足条件的x( )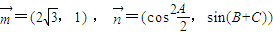 ,其中A,B,C是△ABC的内角.
,其中A,B,C是△ABC的内角.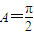 时,求
时,求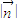 的值
的值 ,当
,当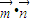 取最大值时,求A大小及AC边长.
取最大值时,求A大小及AC边长. ,其中A、B、C三点共线,则满足条件的x( )
,其中A、B、C三点共线,则满足条件的x( )