题目内容
设指数函数f（x）=ax（a＞0，a≠1），则下列等式中不正确的是
- A.f（x+y）=f（x）•f（y）
- B.
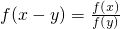
- C.f（nx）=[f（x）]n（n∈Q）
- D.f（xy）n=[f（x）]n•[f（y）]n（n∈N+）
D
分析：利用指数幂的四则运算法则去判断．
解答：A．f（x+y）=ax+y，f（x）•f（y）=ax?ay=ax+y，所以A正确．
B.
，所以B正确．
C．f（nx）=anx=（ax）n=[f（x）]n，所以C正确．
D．[f（xy）]n=（axy）n=（ax）n（ay）=[f（x）]n?f（y），所以D错误．
故选D．
点评：本题主要考查指数幂的四则运算．同底数幂的四则运算法则要求熟练掌握．
分析：利用指数幂的四则运算法则去判断．
解答：A．f（x+y）=ax+y，f（x）•f（y）=ax?ay=ax+y，所以A正确．
B.
，所以B正确．C．f（nx）=anx=（ax）n=[f（x）]n，所以C正确．
D．[f（xy）]n=（axy）n=（ax）n（ay）=[f（x）]n?f（y），所以D错误．
故选D．
点评：本题主要考查指数幂的四则运算．同底数幂的四则运算法则要求熟练掌握．
练习册系列答案
相关题目
设指数函数f（x）=ax（a＞0且a≠1），则下列等式不正确的是（ ）
| A、f（x+y）=f（x）•f（y） | ||
| B、f[（xy）n]=[f（x）]n•[f（y）]n | ||
C、f（x-y）=
| ||
| D、f（nx）=[f（x）]n |