题目内容
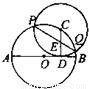
 如图,已知AB圆O的直径,C、D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.
如图,已知AB圆O的直径,C、D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.(Ⅰ)求证:C是劣弧BD的中点;
(Ⅱ)求证:BF=FG.
分析:(I)要证明C是劣弧BD的中点,即证明弧BC与弧CD相等,即证明∠CAB=∠DAC,根据已知中CF=FG,AB是圆O的直径,CE⊥AB于E,我们易根据同角的余角相等,得到结论.
(II)由已知及(I)的结论,我们易证明△BFC及△GFC均为等腰三角形,即CF=BF,CF=GF,进而得到结论.
(II)由已知及(I)的结论,我们易证明△BFC及△GFC均为等腰三角形,即CF=BF,CF=GF,进而得到结论.
解答:解:(I)∵CF=FG
∴∠CGF=∠FCG
∴AB圆O的直径
∴∠ACB=∠ADB=
∵CE⊥AB
∴∠CEA=
∵∠CBA=
-∠CAB,∠ACE=
-∠CAB
∴∠CBA=∠ACE
∵∠CGF=∠DGA
∴∠DGA=∠ABC∴
-∠DGA=
-∠ABC
∴∠CAB=∠DAC
∴C为劣弧BD的中点(5分)
(II)∵∠GBC=
-∠CGB,∠FCB=
-∠GCF
∴∠GBC=∠FCB
∴CF=FB
同理可证:CF=GF
∴BF=FG(10分)
∴∠CGF=∠FCG
∴AB圆O的直径
∴∠ACB=∠ADB=
| π |
| 2 |
∵CE⊥AB
∴∠CEA=
| π |
| 2 |
∵∠CBA=
| π |
| 2 |
| π |
| 2 |
∴∠CBA=∠ACE
∵∠CGF=∠DGA
∴∠DGA=∠ABC∴
| π |
| 2 |
| π |
| 2 |
∴∠CAB=∠DAC
∴C为劣弧BD的中点(5分)
(II)∵∠GBC=
| π |
| 2 |
| π |
| 2 |
∴∠GBC=∠FCB
∴CF=FB
同理可证:CF=GF
∴BF=FG(10分)
点评:本题考查的知识点圆周角定理及其推理,同(等)角的余角相等,其中根据AB是圆O的直径,CE⊥AB于E,找出要证明相等的角所在的直角三角形,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
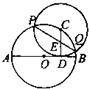 11、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是
11、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是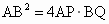 .
.