题目内容
边长为1的等边三角形AOB,O为原点,AB⊥x轴,以O为顶点且过A、B的抛物线方程是( )A.y2=![]() x B.y2=
x B.y2=![]() x
x
C.y2=±![]() x D.y2=±
x D.y2=±![]() x
x
思路分析:∵△AOB为边长等于1的正三角形,∴O到AB的距离为![]() ,A或B到x轴的距离为
,A或B到x轴的距离为![]() ,当抛物线的焦点在x轴的正半轴上时,设抛物线的方程为y2=2px(p>0),
,当抛物线的焦点在x轴的正半轴上时,设抛物线的方程为y2=2px(p>0),
∵抛物线过点(![]() ),∴(
),∴(![]() )2=2p·
)2=2p·![]() ,∴2p=
,∴2p=![]() ,
,
∴抛物线的方程为y2=![]() x;
x;
当抛物线的焦点在x轴的负半轴上时,设抛物线的方程为y2=-2px(p>0),
∵抛物线过点(![]() ),∴(
),∴(![]() )2=-2p·(
)2=-2p·(![]() ),∴2p=
),∴2p=![]() ,∴抛物线的方程为y2=
,∴抛物线的方程为y2=![]() x.
x.
答案:C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
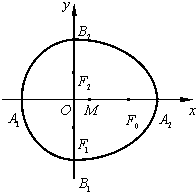 附加题:已知半椭圆
附加题:已知半椭圆 ,已知
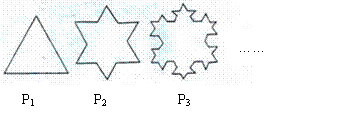
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求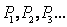 ,已知
,已知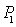 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对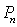 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
(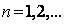 ),求
),求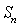 为曲线
为曲线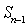 的递推关系式,并求
的递推关系式,并求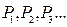 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求