Question

已知函数f（x）=（sinx+cosx）²
（1）求函数f（x）的最小正周期，并用“五点法”作出函数f（x）在一个周期内的简图；
（2）求函数f（x）的最大值，以及使函数f（x）取得最大值时x的集合．

Answer 1

分析：利用平方和公式和二倍角公式，将f（x）解析式化为f（x）=sin²x+2sinx•cosx+cos²x=1+sin2x，
（1）T=

2π

2

=π，令2x=0，

π

4

，  

π

2

，

3π

4

，π，得出相应的点（x，y），描点连线，
（2）f（x）取得最大值的充要条件是sin2x=1，2x=

π

2

+2kπ，k∈Z，即x=

π

4

+kπ．k∈Z．

解答：解：（!）f（x）=sin²x+2sinx•cosx+cos²x=1+sin2x∴T=π．
列表
描点连线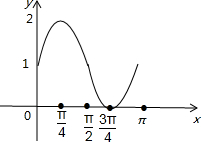
（2）f（x）取得最大值的充要条件是sin2x=1，f（x）的最大值是2．此时2x=

π

2

+2kπ，k∈Z，x=

π

4

+kπ．
∴函数f（x）取得最大值时x的集合是{x|x=

π

4

+kπ，k∈Z}．

点评：此类题目将所给的函数式化简为y=Asin（ωx+φ）+k，那么其相关的性质很容易得知．