题目内容
三棱锥P—ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3.
(1)求证:AB⊥BC;
(2)如果AB=BC=![]() ,求侧面PBC与侧面PAC所成二面角的大小.
,求侧面PBC与侧面PAC所成二面角的大小.
(1)证明:如图,取AC的中点D,连结PD、BD.

因为PA=PC,所以PD⊥AC.
又已知面PAC⊥面ABC,所以PD⊥面ABC,D为垂足.
因为PA=PB=PC,
所以DA=DB=DC.可知AC为△ABC的外接圆直径,因此AB⊥BC.
(2)解:
因为AB=BC,D为AC的中点,所以BD⊥AC.
又面PAC⊥面ABC,所以BD⊥平面PAC,D为垂足.
作BE⊥PC于点E,连结DE,
因为DE为BE在平面PAC内的射影,
所以DE⊥PC,∠BED为所求二面角的平面角.
在Rt△ABC中,AB=BC=![]() ,所以BD=
,所以BD=![]() .
.
在Rt△PDC中,PC=3,DC=![]() ,PD=
,PD=![]() ,
,
所以DE=![]() .
.
因此,在Rt△BDE中,tan∠BED=![]() =
=![]() ,∠BED=60°,
,∠BED=60°,
所以侧面PBC与侧面PAC所成的二面角为60°.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.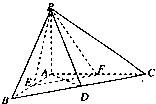 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,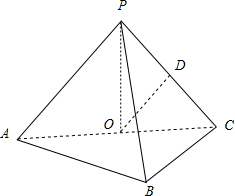 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.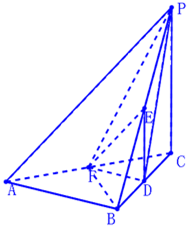 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.