题目内容
命题P：实数x满足x2-4ax+3a2＜0（其中a＜0），命题Q：实数x满足x2+6x+8≥0，且￢p是￢q的必要不充分条件，求实数a的取值范围．
分析：利用不等式的解法求解出命题p，q中的不等式范围问题，结合二者的关系得出关于字母a的不等式，从而求解出a的取值范围．
解答：解：命题P：A=（3a，a），命题Q：B=（-∞，-4]∪[-2，+∞）．…（4分）
∵?p是?q的必要不充分条件
∴p是q的充分不必要条件即A是B的真子集．…（8分）
∴a≤-4或-2≤3a＜a＜0
∴a的取值范围是(-∞，-4]∪[-
，0)．…（12分）
∵?p是?q的必要不充分条件
∴p是q的充分不必要条件即A是B的真子集．…（8分）
∴a≤-4或-2≤3a＜a＜0
∴a的取值范围是(-∞，-4]∪[-
| 2 |
| 3 |
点评：本题考查必要条件、充分条件与充要条件的判断，一元二次不等式的解法，考查二次不等式与二次函数的关系，注意等价转化思想的运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
．
．
．
．
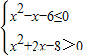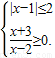
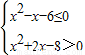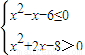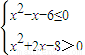