题目内容
(本小题满分12分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足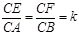 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 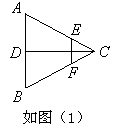
(Ⅰ) 求二面角B-AC-D的大小;
(Ⅱ) 若异面直线AB与DE所成角的余弦值为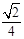 ,求k的值.
,求k的值.
(1) 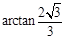 . (2) k=
. (2) k=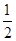
解析试题分析:解:(Ⅰ) 过D点作DG⊥AC于G,连结BG,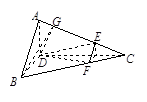
∵ AD⊥CD, BD⊥CD,
∴ ∠ADB是二面角A-CD-B的平面角.
∴ ∠ADB=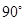 , 即BD⊥AD.
, 即BD⊥AD.
∴ BD⊥平面ADC. ∴ BD⊥AC.
∴ AC⊥平面BGD. ∴ BG⊥AC .
∴ ∠BGD是二面角B-AC-D的平面角.
在ADC中,AD=a, DC=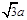 , AC=2a,
, AC=2a,
∴ 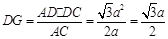 .
.
在Rt△BDG中,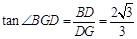 .
.
∴  .
.
即二面角B-AC-D的大小为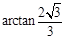 .
.
(Ⅱ) ∵ AB∥EF, ∴ ∠DEF(或其补角)是异面直线AB与DE所成的角.
∵ 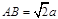 ,∴
,∴ 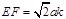 .
.
又DC=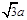 ,
, 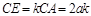 ,
,
∴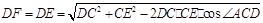
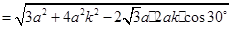
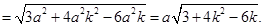
∴ 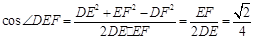 .
.
∴  . 解得 k=
. 解得 k=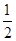 .
.
考点:异面直线所成的角,以及二面角度求解
点评:解决该试题的关键是能利用定义求作角,结合三角形来求解得到结论,属于基础题。

练习册系列答案
相关题目
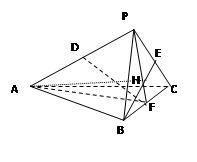

 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点E为
,点E为 的中点。
的中点。


 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。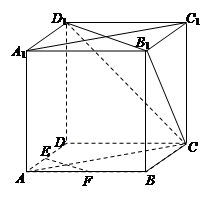
 ,
,
 中,△
中,△ 为等腰直角三角形,∠
为等腰直角三角形,∠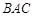 =
=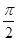 ,且
,且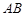 =
=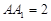 ,
,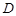 、
、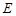 、
、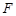 分别为
分别为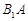 、
、 、
、 的中点.
的中点.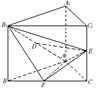
 ∥平面
∥平面 ⊥平面
⊥平面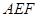 ;
;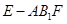 的体积.
的体积.
 中,侧棱
中,侧棱 底面
底面 ,
, ,
,
 ,
,
 与
与 所成角的余弦值;
所成角的余弦值;