题目内容
下列图象中,是一次函数y=ax+b,指数函数y=(
)x和对数函数y=log
x中的两个函数的图象,其中可能正确的是( )
| b |
| a |
| b |
| a |
分析:分别讨论a,b的取值,然后利用指数函数和对数函数的单调性是否对应,确定选项.
解答:解:当y=0时,x=-
,即直线与x轴的横截距为-
.
A中,由直线的图象可知,b>1.横截距-
<-1,所以
>1,此时指数函数应该单调递增,所以A不可能.
B中,直线的横截距-1<-
<0,即0<
<1,此时对数函数应为单调递减函数,所以B不可能.
C中,直线的横截距-1<-
<0,即0<
<1,此时指数函数应为单调递减函数,所以C不可能.
D中,直线的横截距-
<-1,所以
>1,此时对数函数应为单调递减函数,所以D可能.
故选D.
| b |
| a |
| b |
| a |
A中,由直线的图象可知,b>1.横截距-
| b |
| a |
| b |
| a |
B中,直线的横截距-1<-
| b |
| a |
| b |
| a |
C中,直线的横截距-1<-
| b |
| a |
| b |
| a |
D中,直线的横截距-
| b |
| a |
| b |
| a |
故选D.
点评:本题主要考查指数函数和对数函数的图象和单调性的判断,通过直线关系确定a,b的大小关系是解决本题的关键.

练习册系列答案
相关题目
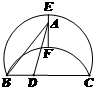 如图E、F是以线段BC为公共弦的两条圆弧的中点,BC=6.点A、D分别为线段EF、BC上的动点.连接AB、AD,设BD=x,AB2-AD2=y,下列图象中,能表示y与x的函数关系的图象是( )
如图E、F是以线段BC为公共弦的两条圆弧的中点,BC=6.点A、D分别为线段EF、BC上的动点.连接AB、AD,设BD=x,AB2-AD2=y,下列图象中,能表示y与x的函数关系的图象是( )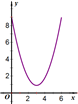
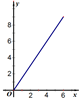
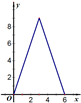

 和对数函数y=
和对数函数y= 中的两个函数的图象,其中可能正确的是
中的两个函数的图象,其中可能正确的是



 和对数函数y=
和对数函数y= 中的两个函数的图象,其中可能正确的是( )
中的两个函数的图象,其中可能正确的是( )


