题目内容
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=| 1 |
| 2 |
| 3 |
（1）求证：平面PQB⊥平面PAD；
（2）若PA∥平面QBM，求
| PM |
| MC |
（3）若
| PM |
| MC |
分析：（1）利用面面垂直的性质，可得线面垂直，再利用面面垂直的判定，可得结论；
（2）利用线面平行，可得线线平行，从而可得比值；
（3）连接CQ，作MF⊥CQ于点F，作FG⊥BQ于点G，连接GM，证明二面角M-BQ-C的平面角为∠MGF，即可求得结论．
（2）利用线面平行，可得线线平行，从而可得比值；
（3）连接CQ，作MF⊥CQ于点F，作FG⊥BQ于点G，连接GM，证明二面角M-BQ-C的平面角为∠MGF，即可求得结论．
解答：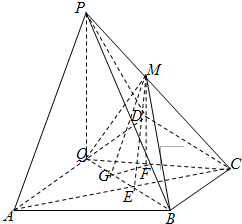
（1）证明：∵DQ∥BC且DQ=BC，∴四边形BCDQ是平行四边形，∴BQ∥CD，
∵CD⊥AD，∴BQ⊥AD，
∵平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，∴BQ⊥平面PAD，
∵BQ?平面PQB，∴平面PQB⊥平面PAD．
（2）解：设AC∩BQ=E，∵PA∥平面QBM，∴PA∥ME，∴
=
=
=1．
（3）解：连接CQ，作MF⊥CQ于点F，作FG⊥BQ于点G，连接GM，
∵MF⊥CQ，PQ⊥CQ，∴PQ∥MF，
∵PQ⊥AD，平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，∴PQ⊥平面ABCD，∴MF⊥平面ABCD，
∵FG⊥BQ，∴BQ⊥MG，∴二面角M-BQ-C的平面角为∠MGF，
∵
=
=
，∴MF=
PQ=
，
∵
=
=
，∴FG=
BC=
，
∴tan∠MGF=
=
，∴∠MGF=
，
∴二面角M-BQ-C的大小为
．
（1）证明：∵DQ∥BC且DQ=BC，∴四边形BCDQ是平行四边形，∴BQ∥CD，∵CD⊥AD，∴BQ⊥AD，
∵平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，∴BQ⊥平面PAD，
∵BQ?平面PQB，∴平面PQB⊥平面PAD．
（2）解：设AC∩BQ=E，∵PA∥平面QBM，∴PA∥ME，∴
| PM |
| MC |
| AE |
| EC |
| AQ |
| BC |
（3）解：连接CQ，作MF⊥CQ于点F，作FG⊥BQ于点G，连接GM，
∵MF⊥CQ，PQ⊥CQ，∴PQ∥MF，
∵PQ⊥AD，平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，∴PQ⊥平面ABCD，∴MF⊥平面ABCD，
∵FG⊥BQ，∴BQ⊥MG，∴二面角M-BQ-C的平面角为∠MGF，
∵
| MF |
| PQ |
| CM |
| CP |
| 1 |
| 4 |
| 1 |
| 4 |
| ||
| 4 |
∵
| FG |
| BC |
| QF |
| QC |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴tan∠MGF=
| MF |
| FG |
| ||
| 3 |
| π |
| 6 |
∴二面角M-BQ-C的大小为
| π |
| 6 |
点评：本题考查面面垂直的性质与判定，考查线面平行，考查面面角，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=3，AD=2，PA=2，PD=2
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB=4，PA=3，点A在PD上的射影为点G，点E在AB上，平面PEC⊥平面PDC．
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠BCD=120°，BC⊥AB，CD⊥AD，BC=CD=PA=a，
如图，在四棱锥P-ABCD中，底面是边长为a的菱形，∠ABC=60°PD⊥面ABCD，PC=a，E为PB中点
（2008•武汉模拟）如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，BC∥AD，且∠BAD=90°，又PA⊥底面ABCD，BC=AB=PA=1，AD=2．