题目内容
（本小题满分12分）已知三次函数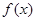
的导函数
，
，
．
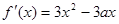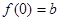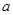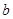为实数.
（1）若曲线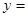
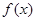在点（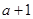
，
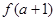）处切线的斜率为12，求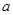的值；
（2）若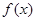在区间［-1，1］上的最小值．最大值分别为-2．1，且
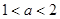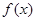，求函数的解析式.
【答案】
（Ⅰ）
；（Ⅱ）
=
。
【解析】(1)根据
可得a值.
（2）由 
，
，得
然后再根据
得x=0,x=a,再结合
易求f(x)的单调区间，进而可得到其极值最值,从而得到关于a,b的方程，解出a值，b值,解析式确定.
（Ⅰ）由导数的几何意义
=12
∴ 
∴ 
∴ ………………………4分
（Ⅱ）∵ ， ∴
由 
得
，
∵ 
［-1，1］，
∴ 当［-1，0）时，
，递增；
当（0，1］时，
，递减.……………8分
∴ 在区间［-1，1］上的最大值为
∵ ，∴ 
=1
……………………10分
∵ 
，
∴ 
∴ 
是函数的最小值，
∴ 
∴ 
∴ = .................12分
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
