题目内容
(12分)已知函数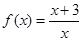 :
:
(1)写出此函数的定义域和值域;
(2)证明函数在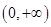 为单调递减函数;
为单调递减函数;
(3)试判断并证明函数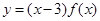 的奇偶性.
的奇偶性.
【答案】
(1) (2)见解析(3)奇函数
(2)见解析(3)奇函数
【解析】
试题分析:(1)显然定义域为 .
……3分
.
……3分
因为 ∴值域为
∴值域为 ……6分
……6分
(2)设 ,
,
则: ,
,
 ∴
∴ ,
, ,
,
∴ ,
,
∴函数在 为单调递减函数.
……9分
为单调递减函数.
……9分
(3)显然函数定义域关于原点对称,
设 ,
, ,
,
∴此函数为奇函数. ……12分
考点:本小题主要考查函数定义域、值域的求法,用定义证明单调性以及函数奇偶性的判断.
点评:用定义证明单调性时一定要把结果化到最简,判断函数奇偶性时,要先看函数的定义域是否关于原点对称.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |