题目内容
已知定点![]() 和定直线
和定直线![]() ,
,![]() 是定直线
是定直线![]() 上的两个动点且满足
上的两个动点且满足![]() ,动点
,动点![]() 满足
满足![]() ,
,![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点
两点
①求![]() 的值;
的值;
②设![]() ,当三角形
,当三角形![]() 的面积
的面积![]() 时,求
时,求![]() 的取值范围.
的取值范围.
![]() ;
;![]() ;
; ![]()
解析:
(1)设![]() (
(![]() 均不为
均不为![]() ),
),
由![]() ∥
∥![]() 得
得![]() ,即
,即![]()
由![]() ∥
∥![]() 得
得![]() ,即
,即![]()
![]()
得 ![]()
![]()
动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
(2)①由(1)得![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ,
,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,将其与
,将其与![]() 的方程联立,消去
的方程联立,消去![]() 得
得![]() . 设
. 设![]() 的坐标分别为
的坐标分别为![]() ,则
,则![]() .
. ![]() , 9分
, 9分
故![]()
②解法一:![]() , 即
, 即
![]() 又
又![]() ,
, ![]() .
. ![]() 可得
可得![]()
故三角形![]() 的面积
的面积![]() ,
,
因为![]() 恒成立,所以只要解
恒成立,所以只要解![]() .
.
即可解得![]() .
.
解法二:![]() ,
,![]()
![]() ,
,
![]() (注意到
(注意到![]() )
)
又由①有![]() ,
,![]() ,
,![]()
三角形![]() 的面积
的面积![]() (以下解法同解法一)
(以下解法同解法一)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是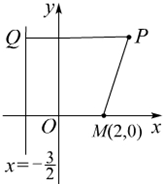 已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=
已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=