题目内容
在正方体ABCD-A1B1C1D1中，E、F分别为BB1、CD的中点，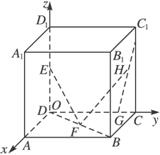
（1）求证：D1F⊥平面ADE；
（2）判断A、D、C1、E四点是否共面，请说明理由.
（1）证明：以DA、DC、DD1为x、y、z轴建系如图：
设正方体棱长为1,则D（0，0，0），D1（0，0，1）.
A（1，0，0），E（1，1，
），F（0，
，0）.
=（0，
，-1），
=（1，0，0），
=（0，1，
）,
·
=0，
·
=
-
=0.
∴D1F⊥DA，D1F⊥AE,又DA∩AE=A,即D1F⊥面ADE.
（2）解析:
=（1，0，0），
=（0，1，1），
=（1，1，
）.
设
=x
+y
，则
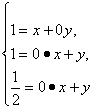无解.
即不存在实数x，y满足
=x
+y
.
∴
、
、
不共面.∴D、A、C1、E不共面.
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）