题目内容
已知向量 与向量
与向量 ,|
,| |=2,|
|=2,| |=3,
|=3, 、
、 的夹角为60°,当1≤m≤2,0≤n≤2时,|m
的夹角为60°,当1≤m≤2,0≤n≤2时,|m +n
+n |的最大值为________.
|的最大值为________.
10
分析:依题意,欲求|m +n
+n |的最大值,需求
|的最大值,需求 的最大值,利用向量的数量积可求得
的最大值,利用向量的数量积可求得 的关系式,再结合1≤m≤2,0≤n≤2,即可求得答案.
的关系式,再结合1≤m≤2,0≤n≤2,即可求得答案.
解答:∵| |=2,|
|=2,| |=3,
|=3, 、
、 的夹角为60°,
的夹角为60°,
∴ =m2
=m2 +2mn
+2mn •
• +n2
+n2 =4m2+2mn×2×3×cos60°+9n2=4m2+6mn+9n2,
=4m2+2mn×2×3×cos60°+9n2=4m2+6mn+9n2,
∵1≤m≤2,0≤n≤2,
∴当m=2且n=2时, 取到最大值,即
取到最大值,即 =100,
=100,
∴,|m +n
+n |的最大值为10.
|的最大值为10.
故答案为:10.
点评:本题考查数量积表示两个向量的夹角,考查向量的模,考查分析与运算能力,属于中档题.
分析:依题意,欲求|m
 +n
+n |的最大值,需求
|的最大值,需求 的最大值,利用向量的数量积可求得
的最大值,利用向量的数量积可求得 的关系式,再结合1≤m≤2,0≤n≤2,即可求得答案.
的关系式,再结合1≤m≤2,0≤n≤2,即可求得答案.解答:∵|
 |=2,|
|=2,| |=3,
|=3, 、
、 的夹角为60°,
的夹角为60°,∴
 =m2
=m2 +2mn
+2mn •
• +n2
+n2 =4m2+2mn×2×3×cos60°+9n2=4m2+6mn+9n2,
=4m2+2mn×2×3×cos60°+9n2=4m2+6mn+9n2,∵1≤m≤2,0≤n≤2,
∴当m=2且n=2时,
 取到最大值,即
取到最大值,即 =100,
=100,∴,|m
 +n
+n |的最大值为10.
|的最大值为10.故答案为:10.
点评:本题考查数量积表示两个向量的夹角,考查向量的模,考查分析与运算能力,属于中档题.

练习册系列答案
相关题目
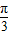 ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于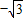
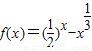 在区间(0,1)上存在零点.
在区间(0,1)上存在零点.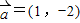 与向量
与向量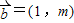 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是(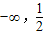 )
) ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于
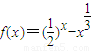 在区间(0,1)上存在零点.
在区间(0,1)上存在零点. 与向量
与向量 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是( )
)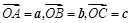 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若
 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算 ,显然
,显然 的结果仍为一向量,记作
的结果仍为一向量,记作 .
. 的法向量;
的法向量; 为边的平行四边形
为边的平行四边形 的面积等于
的面积等于 ;
; 平移,得到一个平行六面体
平移,得到一个平行六面体 ,试判断平行六面体的体积
,试判断平行六面体的体积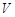 与
与 的大小.
的大小.
 与向量
与向量 平行,则
平行,则 等于
等于 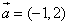 ,点A(8,0),B(n,t),
,点A(8,0),B(n,t),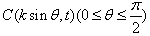 。
。 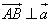 ,且
,且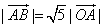 ,求向量
,求向量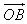 ;
;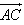 与向量
与向量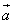 共线,当k>4时,tsinθ的最大值为4,求
共线,当k>4时,tsinθ的最大值为4,求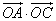 的值。
的值。