题目内容
定义:同时满足下列两个条件的数列{an} 叫做“上凸有界数列”,①| an+an+2 | 2 |
(I)若数列{an} 的前n项和为Sn,且Sn=2n-1,试判断数列{an} 是否为上凸有界数列;
(Ⅱ)若数列{bn}是等差数列,Tn为其前n项和,且b3=4,T3=18,试证明:数列{Tn}为上凸有界数列.
分析:(I)利用公式an=
求得数列{an}的通项公式,易知此数列不满足条件②
(II)设设{bn}的公差为d的公差为d,列方程求得首相和公差,得{bn}的通项公式,进而求和得Tn,利用作差法可证的满足条件①,利用数列的函数性质,可证得满足条件②
|
(II)设设{bn}的公差为d的公差为d,列方程求得首相和公差,得{bn}的通项公式,进而求和得Tn,利用作差法可证的满足条件①,利用数列的函数性质,可证得满足条件②
解答:解:(I)n=1时,a1=s1=2-1=1
n≥2时an=sn-sn-1=2n-1-(2n-1-1)=2n-1
∴an=2n-1
显然an=2n-1是递增数列,故不存在常数M,使an≤M成立
∴数列{an} 不是上凸有界数列
(II)设{bn}的公差为d,则
解得b1=8,d=-2
∴Tn=8n+
(-2)=-n2+9n
∵
-Tn+1=
=
=
=-1<0
∴
≤Tn+1,即{Tn}满足条件①
又Tn=-n2+9n=-(n-
)2+
当n=4或5时Tn取最大值20,即Tn≤20,满足条件②
综上数列{Tn}为上凸有界数列
n≥2时an=sn-sn-1=2n-1-(2n-1-1)=2n-1
∴an=2n-1
显然an=2n-1是递增数列,故不存在常数M,使an≤M成立
∴数列{an} 不是上凸有界数列
(II)设{bn}的公差为d,则
|
解得b1=8,d=-2
∴Tn=8n+
| n(n-1) |
| 2 |
∵
| Tn+Tn+2 |
| 2 |
| (Tn+2-Tn+1)-(Tn+1-Tn) |
| 2 |
| bn+2-bn+1 |
| 2 |
| d |
| 2 |
∴
| Tn+Tn+2 |
| 2 |
又Tn=-n2+9n=-(n-
| 9 |
| 2 |
| 81 |
| 4 |
当n=4或5时Tn取最大值20,即Tn≤20,满足条件②
综上数列{Tn}为上凸有界数列
点评:本题综合考查了数列通项公式的求法,数列求和的方法以及数列的函数性质

练习册系列答案
相关题目
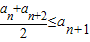 ②an≤M,M是与n无关的常数.
②an≤M,M是与n无关的常数.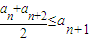 ②an≤M,M是与n无关的常数.
②an≤M,M是与n无关的常数.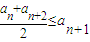 ②an≤M,M是与n无关的常数.
②an≤M,M是与n无关的常数.