题目内容
已知函数f(x)=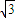 asinωx-acosωx
asinωx-acosωx(a>0,ω>0)的图象上两相邻最高点与最低点的坐标分别为(
 ,2),(
,2),(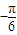 ,-2).
,-2).(Ⅰ)求a与ω的值;
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且f(A)=2,求
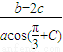 的值.
的值.
【答案】分析:(Ⅰ)利用两角和差的正弦公式把f(x)的解析式化为2asin(ωx- ),从而求出它的周期.
),从而求出它的周期.
(Ⅱ)由f(A)=2,求得A= =600 ,再根据正弦定理把要求的式子化为
=600 ,再根据正弦定理把要求的式子化为 ,再利用两角和差的正弦、余弦公式进一步化为
,再利用两角和差的正弦、余弦公式进一步化为 ,
,
约分整理求得最后的结果.
解答:解:(Ⅰ)f(x)= asinωx-acosωx=2asin(ωx-
asinωx-acosωx=2asin(ωx- ),由已知知周期T=2[
),由已知知周期T=2[ -(
-( )]=π=
)]=π= ,∴ω=2.
,∴ω=2.
又最大值为2,故2a=2,∴a=1.…(6分)
(Ⅱ)由f(A)=2,即sin(2A- )=1,∵0<A<π,∴-
)=1,∵0<A<π,∴- <2A-
<2A- <
< ,则2A-
,则2A- =
= ,解得A=
,解得A= =60.
=60.
故 =
= =
=
= =
= =2.(也可用B化简)…(12分)
=2.(也可用B化简)…(12分)
点评:本题主要考查正弦定理、两角和差的正弦、余弦公式的应用,y=Asin(ωx+∅)的周期性,根据三角函数的值求角,属于中档题.
 ),从而求出它的周期.
),从而求出它的周期.(Ⅱ)由f(A)=2,求得A=
 =600 ,再根据正弦定理把要求的式子化为
=600 ,再根据正弦定理把要求的式子化为 ,再利用两角和差的正弦、余弦公式进一步化为
,再利用两角和差的正弦、余弦公式进一步化为 ,
,约分整理求得最后的结果.
解答:解:(Ⅰ)f(x)=
 asinωx-acosωx=2asin(ωx-
asinωx-acosωx=2asin(ωx- ),由已知知周期T=2[
),由已知知周期T=2[ -(
-( )]=π=
)]=π= ,∴ω=2.
,∴ω=2.又最大值为2,故2a=2,∴a=1.…(6分)
(Ⅱ)由f(A)=2,即sin(2A-
 )=1,∵0<A<π,∴-
)=1,∵0<A<π,∴- <2A-
<2A- <
< ,则2A-
,则2A- =
= ,解得A=
,解得A= =60.
=60.故
 =
= =
=
=
 =
= =2.(也可用B化简)…(12分)
=2.(也可用B化简)…(12分)点评:本题主要考查正弦定理、两角和差的正弦、余弦公式的应用,y=Asin(ωx+∅)的周期性,根据三角函数的值求角,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目